เรื่องและภาพโดย วริศา ใจดี
เนื่องในโอกาสเดือนแห่งความรัก สาระวิทย์ในศิลป์ฉบับเดือนกุมภาพันธ์นี้ ฉันมีเรื่องราวสุดแสนโรแมนติกที่ไม่เพียงแต่จะสร้างความบันเทิงขณะอ่าน แต่ยังมาพร้อมคำถามให้เราฉุกคิดถึงจักรวาลที่เราอาศัยอยู่ นิยายรักที่เกี่ยวข้องกับเรื่องราววิทยาศาสตร์เรื่องนี้จะเป็นอย่างไร ทำใจสบายๆ คิดเสียว่าวันนี้เราพักสมองจากบทความวิชาการ แล้วมาอ่านเรื่องหวานๆ รับวันแห่งความรักกันดูบ้าง
ช่วงปิดเทอมฤดูหนาวที่เพิ่งผ่านมา ฉันได้อ่านนิยายรักเรื่อง Flatland: A Romance of Many Dimensions แต่งเรื่องและวาดภาพประกอบโดย คุณ Edwin A. Abbott ซึ่งเป็นเรื่องราวเกี่ยวกับชีวิตในโลกสองมิติและการผจญภัยเพื่อค้นหาความจริงของมิติอื่นๆ ภายใต้มุมมองของ A Square หรือคุณจัตุรัส A พระเอกของนิยายเรื่องนี้

หน้าปกนิยายเรื่อง Flatland: A Romance of Many Dimensions โดยคุณ Edwin A. Abbott
วันนี้ฉันจะไม่สปอยล์หรอกว่าเรื่องราวสุดแปลกนี้เป็นอย่างไร ถ้าเพื่อนๆ สนใจอยากอ่านเรื่องราวฉบับเต็มสามารถกดเข้าไปอ่านได้ที่ https://www.gutenberg.org/files/201/201-h/201-h.htm แต่บอกได้เลยว่าบทบาทของคุณจัตุรัส A ไม่ได้มีแค่ในนิยายนี้เท่านั้น แต่แทบจะทุกบทของวิชาทอพอโลยี (Topology[1]) ที่ฉันได้เรียนมา
และนี่ก็เป็นหนึ่งสาเหตุที่ศาสตราจารย์วิชาคณิตศาสตร์ของฉันแนะนำนิยายเรื่องนี้มานั่นแหละ! เพราะถ้าฉันไม่ได้รู้จักคุณจัตุรัส A มาก่อน การอ่านนิยายเรื่องนี้คงไม่ต่างอะไรจากการถอดรหัสลับจากนอกโลกเป็นแน่
ดังนั้น! วันนี้ฉันเลยจะมาแนะนำคุณจัตุรัส A (ตามที่ฉันรู้จักผ่านบทเรียน) ให้ทุกคนได้รู้จักกัน ถือเป็นน้ำจิ้มก่อนไปอ่านนิยายจริงๆ จะได้อินกันลงไงล่ะ
ก่อนอื่นต้องขอแนะนำพระเอกของเรื่องเสียก่อน นี่คือหน้าตาของคุณจัตุรัส A
เขาอาศัยอยู่ที่โลก Flatland ดินแดนพื้นที่ราบสองมิติที่ไร้จุดสิ้นสุด
คุณจัตุรัส A ใน Flatland ดินแดนพื้นที่ราบ
แต่โลกไม่ได้มีเพียงแค่ Flatland หากยังมี Pointland ดินแดนพื้นที่ศูนย์มิติ, Lineland ดินแดนพื้นที่หนึ่งมิติ และที่ขาดไม่ได้คือโลกที่ฉันและผู้อ่านทุกคนอาศัยอยู่ก็คือ Spaceland ดินแดนพื้นที่สามมิติ ซึ่งในที่นี้ สิ่งมีชีวิตทั้งหลายจะมีมิติตามสถานที่ที่พวกเขาได้เกิดขึ้นมา เช่น คุณจัตุรัส A ในพื้นราบ ก็จะมีแค่สองมิติ คือ ความกว้างและความยาว แต่คุณทรงกลม B หรือคุณลูกบาศก์ C ที่อาศัยในโลกสามมิติ จะมีความหนาเพิ่มขึ้นอีกมิติ รวมเป็นสามมิติ
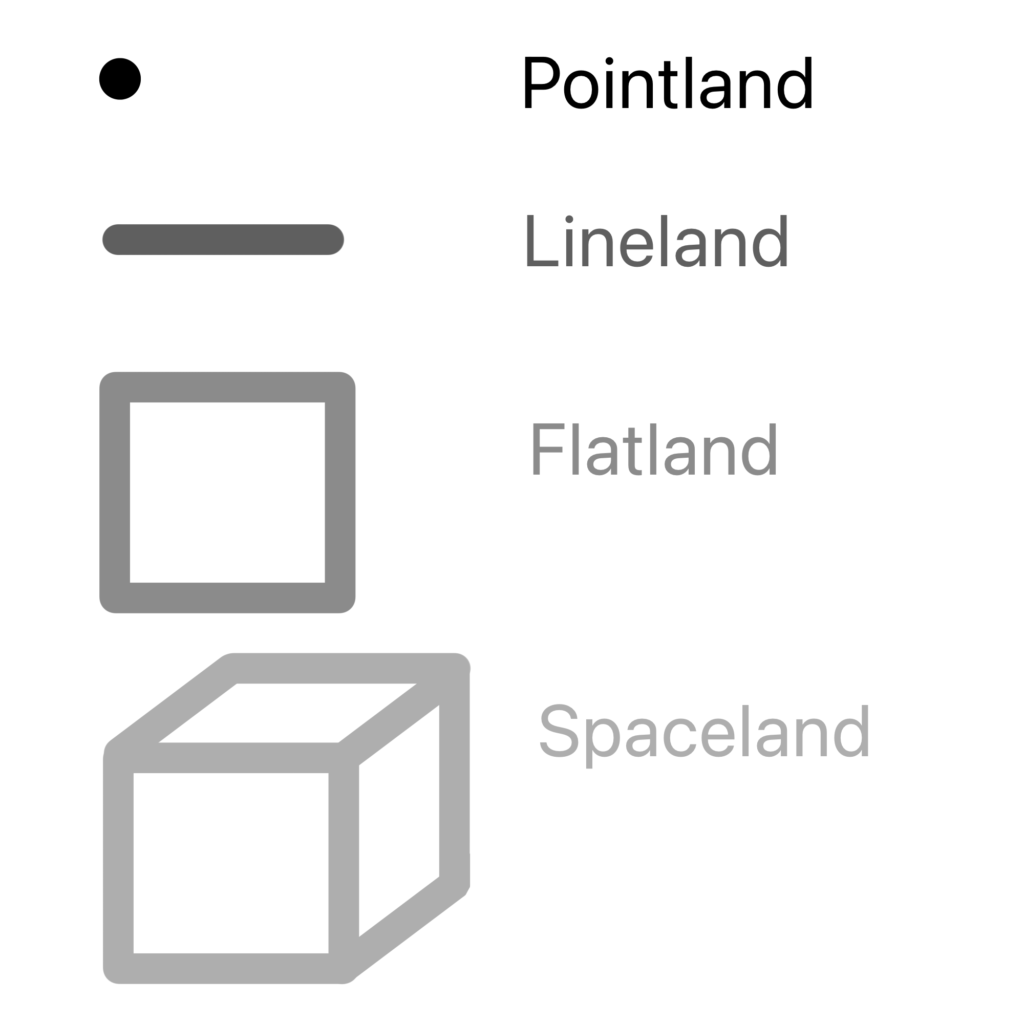
แสดงภาพวาดของดินแดนต่างๆที่ถูกแบ่งตามมิติ
เป็นที่เข้าใจตรงกันว่าในโลกที่แต่ละคนอาศัยอยู่จะไม่มีสิ่งมีชีวิตจากต่างโลกที่มีมิติต่างกันเข้ามาเดินเล่นได้
ไม่เช่นนั้นอาจเกิดเหตุการณ์ดังสถานการณ์สมมติต่อไปนี้ขึ้นมา
คุณจัตุรัส A รู้จักกับคุณทรงกลม B ผ่านการหาคู่ออนไลน์ (online dating) หลังจากที่พูดคุยกันมาเป็นเวลานานนับเดือน คุณจัตุรัส A ก็ตัดสินใจนัดคุณทรงกลม B ให้มาพบกันที่ Flatland ต่างคนต่างตื่นเต้นมากที่จะได้พบเจอตัวจริงกันเป็นครั้งแรก

คุณจัตุรัส A และคุณทรงกลม B กับความรักข้ามมิติของทั้งคู่
และแล้ว…เมื่อถึงวันนัด คุณจัตุรัส A ก็ไปนั่งรอ ณ จุดนัดหมาย แต่รอแล้วรอเล่าก็ไม่มีท่าทีว่าคุณทรงกลม B จะมาพบตามที่นัดหมายกันไว้ คุณจัตุรัส A กลับบ้านไปด้วยความผิดหวังปนงุนงง ต่างฝ่ายต่างมั่นใจว่าไปตามที่นัดตรงตามเวลาเป๊ะๆ แต่ทำไมคุณจัตุรัส A ถึงไม่เห็นคุณทรงกลม B ล่ะ ?! เอ๊ะ หรือว่าตัวจริงของคุณทรงกลม B ไม่ตรงปก
เพื่อตอบคำถามนั้น เราจะมาดูสถานการณ์เมื่อตะกี้อีกที โดยเปรียบเทียบระหว่างมุมมองของคุณจัตุรัส A ตัวแทนสิ่งมีชีวิตบนโลกสองมิติ กับภาพรวมเหตุการณ์ที่คนนอกอย่างเราๆ (สิ่งมีชีวิตสามมิติ) มองเห็น
มุมมองของคุณจัตุรัส A ที่ไม่สามารถรับรู้มิติที่สามหรือความสูงได้ เขาเห็นคุณทรงกลม B เป็นเพียงรูปร่างประหลาดคล้ายเงาที่ฉายลงบนระนาบที่เขาอยู่ เปลี่ยนรูปร่างไปมาขณะที่เวลาดำเนินผ่านไป แล้วหายไป ส่วนมุมมองของคุณทรงกลม B นั้นก็เห็นคุณจัตุรัส A เป็นเพียงแผ่นแบนๆ หรือลวดลายอะไรสักอย่างบนพื้นเท่านั้น
เพราะฉะนั้นจงอย่าคาดหวังมากไปกับการหาคู่ออนไลน์ !
และสิ่งสำคัญที่สุดคือจงอย่าเดตกับสิ่งมีชีวิตที่อยู่ต่างมิติ เพราะสิ่งเดียวที่คุณจะได้เห็นขณะที่คู่เดตของคุณกำลังเดินทางผ่านโลกที่คุณอาศัยอยู่ก็คือ ภาพภาคตัด หรือ cross section ที่ไม่น่าดูซักเท่าไหร่ ดังเงาสีเทาในภาพที่แสดงต่อไปนี้

ภาพแสดงสิ่งที่คุณจัตุรัส A ในระนาบสองมิติมองเห็นขณะที่คุณทรงกลม B สิ่งมีชีวิตสามมิติกำลังเดินทางมาพบกันตามนัด โดยเคลื่อนที่ “ผ่าน” Flatland ที่คุณจัตุรัส A อาศัยอยู่ ลำดับเหตุการณ์ตามเวลาตั้งแต่เที่ยงวัน t=0 ไปจนถึงห้าโมงเย็น t=5 เรียงจากบนลงล่าง เทียบกันซ้ายขวาเฟรมต่อเฟรมระหว่าง 1) มุมมองของคุณจัตุรัส A และ 2) มุมมองโดยรวมจากคนนอกอย่างเราที่เป็นสิ่งมีชีวิตสามมิติ
ดัดแปลงจากหนังสือ Knots, Molecules, and the Universe: an introduction to topology โดยคุณ Erica Flapan
สถานการณ์ที่เกิดขึ้นกับคุณจัตุรัส A ช่วยให้เราเข้าใจจักรวาลมากขึ้น ถึงเราจะแอบขำหน่อยๆ ที่คุณจัตุรัส A เดาไม่ออกว่าสภาพของโลกสองมิตินั้นแตกต่างกับสามมิติอย่างไร แต่เชื่อไหมว่าพวกเราทุกคนก็ไม่ต่างจากคุณจัตุรัส A อาจมีสิ่งมีชีวิตสี่มิติกำลังนั่งดูเราแล้วนำไปใช้เป็นกรณีศึกษาผ่านหนังสือเรียนคณิตศาสตร์ในโลกของเขา และกำลังขำกลิ้งกับการกระทำหลายๆ อย่างของเราอยู่ก็เป็นได้ เป็นไง ขำไม่ออกแล้วใช่ไหมล่ะ
ในเมื่อการศึกษามิติที่สูงขึ้นไปมันทำได้ยากจนแทบจะเป็นไปไม่ได้ นักคณิตศาสตร์เลยใช้วิธีการจำลองสถานการณ์และศึกษามิติในมุมมองของสิ่งมีชีวิตมิติที่ต่ำกว่าอย่างคุณจัตุรัส A มาเป็นกรณีศึกษาให้สิ่งมีชีวิตสามมิติอย่างเราๆ เข้าใจเกี่ยวกับมิติที่สี่ที่อยู่นอกเหนือการรับรู้ของเรา เหมือนกับที่คุณจัตุรัส A ไม่สามารถรับรู้ถึงความเป็นอยู่ของคุณทรงกลม B นั่นแหละ
การศึกษาโดยใช้วิธีการเปรียบเทียบกับสถานการณ์ที่คล้ายคลึงกันแบบนี้ ทำให้มนุษย์เราระลึกขึ้นได้ว่า จักรวาลของเราเองก็อาจมีรูปทรงที่แหวกแนวไปมากกว่ารูปทรงที่เรารู้จักกันอยู่ในชีวิตประจำวัน และอื่นๆ อีกมากมาย
แต่ตราบใดที่ยังไม่มีสิ่งมีชีวิตจากมิติอื่นมาเยือนโลกสามมิติของเรา เราจึงไม่ต้องห่วงว่าจะเผลอหลุดไปสู่เรื่องราวของความรักต้องห้ามข้ามมิติเช่นคุณจัตุรัส A
สวัสดีวันวาเลนไทน์ ขอให้ทุกคนมีความสุขและสมหวังกับความรัก
ที่มาข้อมูล:
อาจารย์คณิตศาสตร์ของฉัน Megan Kerr และหนังสือ Knots, Molecules, and the Universe: an introduction to topology โดยคุณ Erica Flapan
[1] Topology คือสาขาหนึ่งของวิชาคณิตศาสตร์ที่ศึกษาลงลึกเกี่ยวกับคุณสมบัติของวัตถุหรือพื้นที่ว่าง (space) ที่คงอยู่แม้ถูกเปลี่ยนรูป (deformations) เช่น บิดหรือยืดออก เป็นเครื่องมือเชิงคณิตศาสตร์ที่สำคัญทีเดียวสำหรับการทำความเข้าใจจักรวาลและมิติต่างๆ











