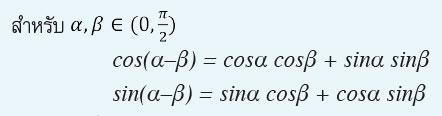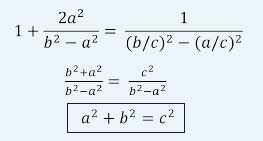วาฟเฟิลโคนกับการค้นพบวิธีพิสูจน์ทฤษฎีบทพีทาโกรัส

เรื่องโดย วีณา เนาวประทีป

เมื่อเร็ว ๆ นี้มีข่าวที่น่าตื่นเต้นในวงการคณิตศาสตร์ นักเรียนมัธยมศึกษาตอนปลาย 2 คน คือ นีคียา ดี. แจ็กสัน (Ne’Kiya D. Jackson) และแคลซี รูเจียน จอห์นสัน (Calcea Rujean Johnson) ค้นพบการพิสูจน์ทฤษฎีบทพีทาโกรัสวิธีใหม่ และนำเสนอบทพิสูจน์นี้ในงาน AMS Spring Southeastern Sectional Meeting ในปี ค.ศ. 2023 ที่ผ่านมา

ทฤษฎีบทพีทาโกรัสเป็นทฤษฎีบทที่แสดงถึงความสัมพันธ์ระหว่างด้านสามด้านของสามเหลี่ยมมุมฉาก นั่นก็คือ

รู้หรือไม่ว่าทฤษฎีบทพีทาโกรัสมีบทพิสูจน์มากมายกว่า 370 บทพิสูจน์ หากย้อนกลับไปเมื่อปี ค.ศ. 1927 เอลิชา สกอตต์ ลูมิส (Elisha Scott Loomis) ได้เขียนหนังสือที่มีชื่อว่า “The Pythagorean Proposition” มีใจความตอนหนึ่งว่า “ไม่มีวิธีการพิสูจน์ทฤษฎีพีทาโกรัสใดที่ใช้ตรีโกณมิติในการพิสูจน์ได้ เนื่องจากว่าตรีโกณมิติมีรากฐานมาจากทฤษฎีบทของพีทาโกรัส ตัวอย่างเช่น ความสัมพันธ์ของเอกลักษณ์ตรีโกณมิติ sin²A+ cos²A = 1 เกิดจากการใช้ทฤษฎีบทพีทาโกรัสกับสามเหลี่ยมมุมฉากในวงกลมหนึ่งหน่วย (unit circle) ในการพิสูจน์” กล่าวง่าย ๆ คือ ไม่สามารถใช้ทฤษฎีบทพีทาโกรัสในการพิสูจน์ได้เพราะความสัมพันธ์นี้เริ่มต้นจากทฤษฎีบทพีทาโกรัส

ต่อมาในปี ค.ศ. 2009 เจสัน ซิมบา (Jason Zimba) ได้พิสูจน์ให้เห็นว่าข้อความนี้ของลูมิสนั้น “ผิด” ซิมบาสามารถพิสูจน์ sin²A+ cos²A = 1 โดยไม่ใช้ทฤษฎีบทพีทาโกรัส ด้วยการพยายามแสดงให้เห็นว่าตรีโกณมิติไม่ได้ขึ้นอยู่กับทฤษฎีบทพีทาโกรัสเสมอไป โดยเริ่มจากแนวคิดสามเหลี่ยมมุมฉากสองรูปที่คล้ายกันจะมีอัตราส่วนของด้านที่สมนัยกันเท่ากัน และเชื่อมความสัมพันธ์ของฟังก์ชันโคไซน์ (cosine) และไซน์ (sine) ดังต่อไปนี้

และล่าสุดในปี ค.ศ. 2023 นีคียากับแคลซีได้นำเสนอบทพิสูจน์ที่สามารถโต้แย้งข้อความของลูมิสว่า “ผิด” เช่นกัน โดยทั้งสองคนได้นำเสนอการพิสูจน์ทฤษฎีบทพีทาโกรัสโดยใช้กฎของไซน์ ซึ่งเป็นตรีโกณมิติ แนวคิดการพิสูจน์นี้ทั้งสองคนเรียกว่า “a waffle cone” โดยเริ่มจากการสร้างชุดสามเหลี่ยมคล้ายที่มีขนาดเล็กลงแบบไม่สิ้นสุด และใช้ผลบวกของอนุกรมเรขาคณิตเพื่อพิสูจน์

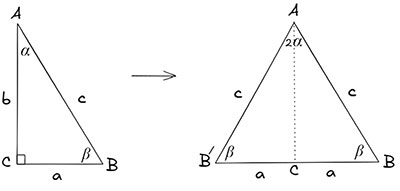
นีคียากับแคลซีเริ่มแนวคิดจากสามเหลี่ยมมุมฉาก ABC ด้านซ้าย หลังจากนั้นสะท้อน (reflect) รูปสามเหลี่ยมมุมฉากมาอีกฝั่งหนึ่งทำให้เกิดสามเหลี่ยมหน้าจั่ว AB’ C รูปด้านขวา

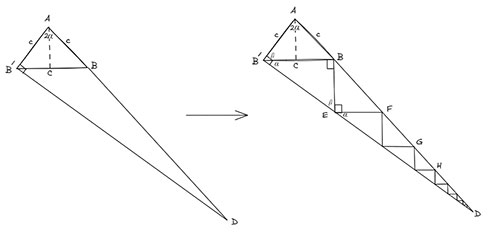
จากรูปสามเหลี่ยมหน้าจั่วก็ได้ลากเส้นจากจุด B และ B’ ไปยัง D เพื่อให้เกิดสามเหลี่ยมมุมฉาก AB’D ดังรูปด้านซ้าย จากนั้นสร้างสามเหลี่ยมคล้ายด้านในสามเหลี่ยม AB’D แบบไม่มีที่สิ้นสุด มีลักษณะคล้ายลายของวาฟเฟิลและนี่จึงเป็นที่มาของการเรียกวิธีพิสูจน์นี้ว่า “a waffle cone” และจากภาพวาฟเฟิลนี้ ทั้งสองคนใช้อัตราส่วนของสามเหลี่ยมคล้าย หาความยาวของด้านดังต่อไปนี้

นี่คือการพิสูจน์แรกที่นีคียากับแคลซีแสดงให้เห็นว่าเราพิสูจน์ทฤษฎีบทพีทาโกรัสได้โดยไม่ต้องใช้ความสัมพันธ์ sin²A+ cos²A = 1 และนำเสนอในงาน AMC Spring Southeastern Sectional Meeting –

ทั้งสองคนตีพิมพ์การพิสูจน์ทฤษฎีบทของพีทาโกรัสทั้งหมด 5 บทพิสูจน์ ในวารสาร The American Mathematical Monthly โดยในบทพิสูจน์ที่เหลือได้ใช้กฎของไซน์เพื่อแสดงให้เห็นว่าเราใช้ตรีโกณมิติในการพิสูจน์ทฤษฎีพีทาโกรัสได้

ความน่าประทับใจจากการค้นพบวิธีการพิสูจน์ใหม่นี้ เริ่มต้นจากนีคียากับแคลซีสนใจส่งผลงานไปร่วมตอบคำถามโบนัสในการแข่งขันคณิตศาสตร์ระดับมัธยมศึกษาของโรงเรียนที่ทั้งสองคนศึกษาอยู่ ซึ่งโจทย์คือ “ให้สร้างวิธีพิสูจน์ใหม่ของทฤษฎีบทพีทาโกรัส” ทั้งสองคนเริ่มต้นจากคิดแค่ว่า ณ ขณะนั้นมีความรู้อะไรบ้างที่รู้อยู่แล้วและน่าจะนำไปใช้พิสูจน์ทฤษฎีบทพีทาโกรัสได้ ซึ่งทั้งสองคนคิดตรงกันว่าน่าจะต้องเริ่มที่อัตราส่วนของสามเหลี่ยมคล้ายและความรู้ต่าง ๆ ที่เกี่ยวข้องกับสามเหลี่ยมมุมฉาก สามเหลี่ยมหน้าจั่ว จากนั้นได้ศึกษาเพิ่มเติมจากวิธีพิสูจน์ของคนอื่นที่ได้รับการยอมรับมาแล้ว

การพิสูจน์ที่นีคียากับแคลซีส่งเข้าประกวดในการแข่งขันที่โรงเรียนก็คือวิธีที่เรียกกันว่า “a waffle cone” นั่นเอง หลังจากนั้นไม่นานคุณครูคณิตศาสตร์ที่เป็นอาสาสมัครในขณะนั้นเรียกทั้งสองไปคุยแล้วบอกว่า การพิสูจน์ของพวกเขานั้นใหม่มากพอที่จะส่งเข้าไปนำเสนอในงานประชุมวิชาการทางคณิตศาสตร์ ทั้งนีคียากับแคลซีเข้าใจว่าครูพูดเล่น เพราะไม่คิดว่าตัวเองที่เป็นแค่เด็กมัธยมและใช้แนวคิดไม่ได้ซับซ้อนอะไรในการพิสูจน์ จะได้รับการยอมรับในระดับนั้น แต่สุดท้าย The AMS Spring Southeastern Sectional Meeting ได้ตอบรับให้ทั้งสองคนไปนำเสนอการพิสูจน์นี้ต่อผู้เข้าร่วมซึ่งส่วนใหญ่เป็นนักคณิตศาสตร์

และจากวันนั้น หลังจากที่เดลลา ดัมบาฟ ( Della Dumbaugh) ซึ่งเป็นบรรณาธิการของวารสาร The American Mathematical Monthly กลับไปที่บ้าน คอลลิน (Colin) ลูกชายของเธอได้เดินมาถามว่า “แม่คิดจะตีพิมพ์งานนี้ลงวารสารหรือไม่” ทำให้เดลลาฉุกคิดและเรียกประชุมทีมบรรณาธิการทันที ทุกคนร่วมมือกันทำงาน โดยช่วยให้คำแนะนำตั้งแต่การใช้ซอฟต์แวร์ LaTex สำหรับจัดพิมพ์เอกสารทางคณิตศาสตร์ซึ่งมีความซับซ้อนสูง ตลอดจนวิธีการเขียนงานวิจัยก่อนที่จะส่งให้ผู้ประเมินบทความ (reviewer) อ่าน และด้วยร่วมมือจากหลายฝ่ายนี้เอง วิธีพิสูจน์ของนีคียากับแคลซีจึงออกมาให้ได้อ่านกันและเป็นแรงบันดาลใจให้แก่เด็กอีกหลายคน

ผู้เขียนได้ฟังบทสัมภาษณ์ของคุณครูที่จัดการแข่งขัน คุณครูให้สัมภาษณ์ว่าสิ่งที่อยากเห็นจากการจัดการแข่งขันนี้คือ “ingenuity” หรือความช่างคิด แนวคิดที่สร้างสรรค์ และ “persistence” ความเพียรพยายามของนักเรียน ไม่ได้คาดหวังว่านักเรียนจะต้องได้วิธีพิสูจน์ใหม่ออกมา สิ่งที่สำคัญคือระหว่างทางนักเรียนได้เรียนรู้อะไรจากการค้นหาและความพยายามสร้างวิธีพิสูจน์ สิ่งที่เกิดขึ้นกับนีคียากับแคลซีนั้นคือผลพลอยได้จากการเรียนรู้ ประกอบกับมีครูและโรงเรียนที่คอยส่งเสริมในทุกด้าน หากครูไม่มีความรู้มากพอจะไม่มีทางรู้เลยว่าสิ่งที่นีคียากับแคลซีเขียนมานั้นคือสิ่งใหม่ ผู้เขียนจึงอยากให้บทความนี้เป็นแรงบันดาลใจให้ทุกคน ไม่จำเป็นต้องจบปริญญาเอกถึงจะสร้างนวัตกรรมได้ อยู่ที่ว่าในระหว่างทางของการเรียนรู้ เรามีความสนใจใคร่รู้ (curiosity) และความพยายามในการหาคำตอบของปัญหามากน้อยแค่ไหน แค่เริ่มจากสิ่งนี้ผู้เขียนเชื่อว่าประเทศไทยก็จะมีนวัตกรคอยสร้างนวัตกรรมให้แก่ประเทศเราเพิ่มขึ้นอีกแน่นอน

แหล่งข้อมูลอ้างอิง

N.D. Jackson and C.R. Johnson. Five or ten new proofs of the Pythagorean theorem. American Mathematical Monthly. Published online October 28, 2024. doi: 10.1080/00029890.2024.2370240.
N.D. Jackson and C.R. Johnson. An impossible proof of Pythagoras. American Mathematical Society Spring Southeastern Sectional Meeting, Atlanta, March 18, 2023.
60 minutes: https://www.youtube.com/watch?v=VHeWndnHuQs