เรื่องโดย
ถกล ตั้งผาติ และนครินทร์ ฉันทะโส
นักสื่อสารวิทยาศาสตร์จากเพจ The Principia และเว็บไซต์ theprincipia.co
ต้นเดือนที่ผ่านมา มีใครซื้อลอตเตอรี่แล้วถูกรางวัลกันบ้างไหมเอ่ย จะถูกรางวัลหรือไม่ อย่างน้อยถ้าอ่านบทความเลขเปลี่ยนโลกก็ยังได้เกร็ดความรู้เล็ก ๆ น้อย ๆ กลับไป ถือว่าไม่ขาดทุน หรือใครจะใช้บทความนี้สำหรับคิดสถิติว่าเลขไหนออกเยอะ เลขไหนออกน้อย ก็ไม่ว่ากัน ถ้าอย่างนั้นเข้าเรื่องกันดีกว่า ในเดือนตุลาคมที่ผ่านมามีเลขท้ายสองตัว 2 งวด ที่เราอยากแนะนำให้รู้จักกับสาระที่ซ่อนอยู่ในตัวเลขเหล่านั้น และในงวดของวันที่ 1 ตุลาคม พ.ศ. 2565 ที่ผ่านมานี้ เลขที่ออกคือ
50
50 เรียกได้ว่าเป็นเลขที่สื่อความหมายกับการเสี่ยงดวงเป็นอย่างมาก เพราะหลาย ๆ ท่านน่าจะเคยได้ยินคำว่า “50/50” สื่ออารมณ์กับตัวเลขต่างกันไป หากไม่เสี่ยงดวงก็อาจจะหมายถึงความไม่มั่นใจ ซึ่งในมุมมองด้านฟิสิกส์หลายคนจะต้องโยงเลขนี้กับทฤษฎีกลศาสตร์ควอนตัม เพราะว่าเป็นทฤษฎีที่มีรากฐานอยู่บนความไม่แน่นอน
แต่วันนี้เราไม่เล่นหนังเรื่องเดิม เพราะในฟิสิกส์มีเรื่องการสุ่มแบบที่หลายคนอาจจะไม่คุ้นเคย ซึ่งแนวความคิดนั้นมีมาก่อนและเป็นส่วนหนึ่งของรากฐานการสร้างทฤษฎีกลศาสตร์ควอนตัมอีกด้วย

ซ้ายมือคือภาพแสดงการเคลื่อนที่ของโมเลกุลก๊าซหนึ่งตัวโดยมีจุดเริ่มต้นจากกึ่งกลางและเคลื่อนที่อย่างสุ่มเมื่อเวลาเปลี่ยนไป แสดงให้เห็นว่าแทบจะเป็นไปไม่ได้เลยที่จะทำนายเส้นทางการเคลื่อนที่ ในขณะที่ขวามือคือแสดงเฉพาะจุดสุดท้ายของโมเลกุลก๊าซหลายโมเลกุลเมื่อเวลาเปลี่ยนไปเท่ากับด้านซ้ายมือ ซึ่งเราจะเริ่มเป็นรูปแบบว่า ส่วนใหญ่แล้วอนุภาคมันจะออกกันตรงกลาง
ที่มาภาพ : https://sethna.lassp.cornell.edu/StatMech/EntropyOrderParametersComplexity20.pdf
เรื่องที่เราจะมานำเสนอวันนี้ก็คือแนวคิดเรื่อง “random walk” แปลตรงตัวคือการเดินแบบสุ่มนั่นเอง
แนวคิดนี้เริ่มต้นมาจากนักฟิสิกส์อยากจะศึกษาพวกอนุภาคหรือโมเลกุลขนาดเล็ก ซึ่งแนวความคิดเรื่องควอนตัมในเวลานั้นยังไม่พัฒนา นักฟิสิกส์จึงใช้จินตนาการคาดเดาเส้นทางการเคลื่อนที่ของอนุภาคก๊าซ หรือการจัดเรียงตัวของสารพอลิเมอร์ เป็นต้น
แน่นอนว่าการจะคาดเดาทิศทางการเคลื่อนที่ของอนุภาคดังกล่าวแทบจะเป็นไปไม่ได้เลยและดูจะยากกว่าการเดาหวยหลายเท่า
จากภาพ random walk ค่อนข้างใช้ในการยืนยันได้ดีว่าการศึกษาการเคลื่อนที่ของอนุภาคหนึ่งตัวในกลุ่มก๊าซเป็นสิ่งที่เป็นไปไม่ได้ดังแสดงในภาพซ้ายมือ แต่หากเราพิจารณาปลายทางของอนุภาคทั้งระบบจะเริ่มเห็นรูปแบบการกระจายตัวว่าส่วนใหญ่อนุภาคมักจะไปกองที่จุดเริ่มต้น (ใจกลาง) และความหนาแน่นของอนุภาคค่อย ๆ น้อยลงจากใจกลางออกมานั่นเอง
ตรงนี้แหละคือที่มาของกลศาสตร์สถิติหรือ statistical mechanics
ดังนั้นเราจะเห็นว่าวิธีการศึกษาระบบในมุมมองของกลศาสตร์สถิตินั้นไม่ใช่การศึกษาที่อนุภาคเดียวอย่างแน่นอนแต่เป็นการศึกษาในกลุ่มหรือระบบที่มีความซับซ้อน ซึ่งเรามีคำภาษาฝรั่งเศสเรียกเฉพาะว่า ensemble ด้วยการถือคติที่ว่าหากการเข้าใจในระบบย่อยอย่างอนุภาคเดี่ยวมันทำได้ยาก ก็ศึกษาจากภาพรวมที่มีมุมมองใหญ่กว่าไปเลย
ถึงแม้ว่าจะเป็นการศึกษาต่อระบบที่สุ่มอย่าง random walk แต่รูปแบบที่เราเห็นนั้นเกิดจากการวิวัฒน์ของระบบ แน่นอนว่าต้องมีสิ่งที่ใช้อธิบายการเปลี่ยนแปลงของระบบนั้น และเราใช้สิ่งที่เรียกว่า เอนโทรปี หรือ entropy
เดิมทีนั้นปริมาณนี้ออกแบบมาให้อธิบายคุณสมบัติทางอุณหพลศาสตร์ของเครื่องยนต์ความร้อนที่เปลี่ยนแปลงไปตามเวลา โดยเครื่องยนต์ความร้อนจะทำงานไปในทิศทางที่การเปลี่ยนแปลงเอนโทรปีมากขึ้น
แต่การขยายขอบเขตและการตีความใหม่ในมุมมองทางวิทยาศาสตร์ปัจจุบันทำให้เอนโทรปีอธิบายการเปลี่ยนแปลงของระบบอื่น ๆ ได้อีกด้วย เช่น การส่งผ่านข้อมูล การรูปแบบการจัดเรียงข้อมูล อีกทั้งยังประยุกต์แนวคิดของเอนโทรปีไปยังการวิวัฒน์ของจักรวาลได้อีกด้วย
หนึ่งในกระบวนการสุ่มที่ใช้ในการศึกษาระบบ random walk คือ ระเบียบวิธี Monte Carlo ซึ่งตั้งชื่อตามเมืองที่มีคาสิโนก้องโลก โดยระเบียบวิธีนี้จะเน้นประยุกต์ใช้กับคอมพิวเตอร์หรือเครื่องคำนวณที่สามารถใช้การสุ่มได้ เพื่อศึกษา ensemble ของระบบที่ซับซ้อนเกินกว่ามนุษย์จะมานั่งทดเลขด้วยตัวเอง ตัวอย่างเช่น ปัญหาในระบบโกลาหล หรือ chaotic system ที่หากเปลี่ยนเงื่อนไขเริ่มต้นจะทำให้คำตอบที่ได้เปลี่ยนไปเป็นคนละทิศคนละทางเลยทีเดียว หนึ่งในตัวอย่างนี้คือ Lorenz system ที่เป็นระบบที่ขึ้นกับตัวแปรแค่สามตัวคือ x, y, และ z โดยมีค่าคงที่ในระบบคือ σ,ρ,β ตามสมการดังนี้
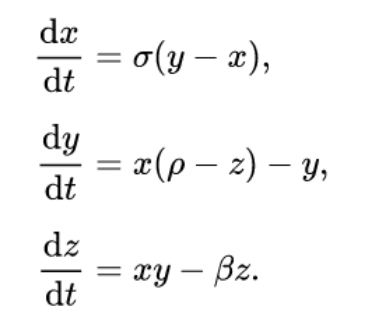
แต่เมื่อทำการเปลี่ยนค่าคงที่ในระบบสมการแค่นิดเดียว คำตอบที่ได้จะเปลี่ยนไปอย่างสิ้นเชิง ดังแสดงในรูปถัดไปนี้
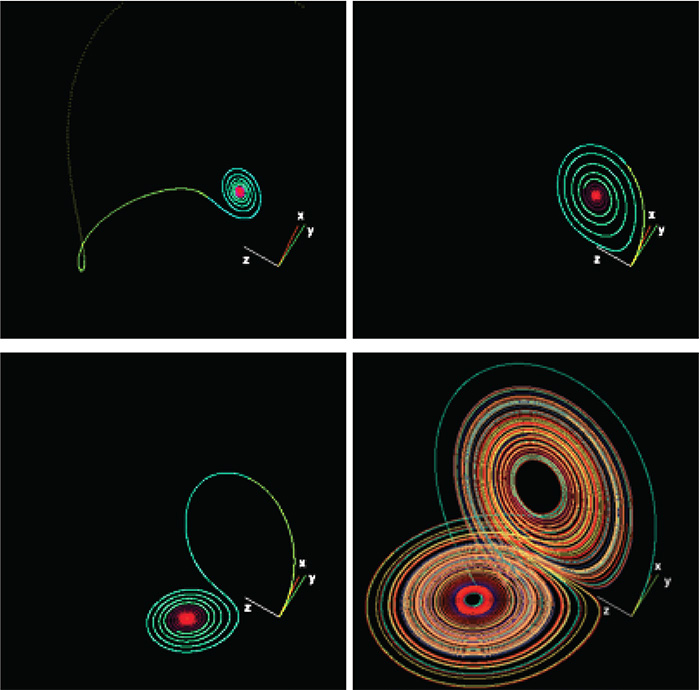
Lorenz system
ที่มาภาพ : https://en.wikipedia.org/wiki/Lorenz_system
หลายคนที่เรียนมาด้านนี้คิดว่าระบบสมการ 3 ตัวแปรและเป็นสมการอนุพันธ์เชิงเส้นแค่นี้แก้ง่าย ๆ อย่าเพิ่งได้ใจไปนะครับ ลองแก้ด้วยตัวเองดูจะพบว่าการแก้หาคำตอบแบบเชิงวิเคราะห์แทบจะทำไม่ได้เลย
ดังนั้นเราไม่อาจทราบคำตอบสุดท้ายว่ามีได้กี่กรณี ทำได้แค่ต้องเปลี่ยนค่าคงที่ไปเรื่อย ๆ เพื่อศึกษารูปแบบของระบบดังแสดงไว้ก่อนหน้า ซึ่งระบบนี้คือระบบอย่างง่ายในการทำนายสภาพอากาศของโลก โดยตัวแปร x คือ อัตราการพาความร้อน, y คือ การเปลี่ยนแปลงอุณหภูมิในแนวนอน และ z คือการเปลี่ยนแปลงอุณหภูมิในแนวตั้ง นี่คือง่ายแล้วนะ ลองจินตนาการความซับซ้อนของระบบสมการปัจจุบันสิครับว่าจะปวดหัวแค่ไหนที่มีปัจจัยอื่น ๆ อีกเพียบ
ทั้งหมดนี้เป็นตัวอย่างเสี้ยวเดียวที่เกี่ยวกับ random walk ไม่ทางตรงก็ทางอ้อม และทั้งหมดนี้อธิบายได้ด้วยวิชากลศาสตร์สถิติหรือ statistical mechanics หวังว่าหลาย ๆ คนที่ได้อ่านบทความนี้ไปน่าจะมีความใคร่รู้ ฉงน สงสัยในวิชาที่มีที่มาจากการศึกษาระบบที่ซับซ้อนไม่มากก็น้อย ต่อไปมาถึงคิวของงวดถัดมาในครึ่งเดือนหลังกันบ้าง กับงวดประจำวันที่ 16 ตุลาคม พ.ศ. 2565 ซึ่งเลขที่ออกได้แก่

15
เมื่อพูดถึงตัวเลข 15 ชวนให้นึกถึงเรื่องราวของนักวิทยาศาสตร์ท่านหนึ่งที่เรียกได้ว่าเมื่อ 2 ปีก่อนเป็นข่าวใหญ่ เมื่อกิตันจาลี เรา (Gitanjali Rao) นักวิทยาศาสตร์วัย 15 ปี (ในขณะนั้น) ได้รับเลือกเป็นเด็กแห่งปีคนแรกของนิตยสารไทม์ เมื่อปี พ.ศ. 2563 จากเยาวชนอเมริกาอายุตั้งแต่ 8-16 ปีที่มีความสนใจในด้านต่าง ๆ กว่า 5,000 คน

กิตันจาลี เรา
ที่มาภาพ : https://commons.wikimedia.org/wiki/File:Rao_Gitanjali_RSI.jpg
กิตันจาลี เรา (Gitanjali Rao) เกิดเมื่อวันที่ 19 พฤศจิกายน ค.ศ. 2005 เธอเป็นชาวอเมริกันเชื้อสายอินเดีย เป็นนักประดิษฐ์ นักเขียน นักวิทยาศาสตร์ ผู้สนับสนุนการศึกษาระบบสะเต็ม (STEM) และนักเคลื่อนไหวทางสังคมผู้สร้างผลงานเอาไว้มากมายไม่ว่าจะเป็นเครื่องตรวจวัดระดับตะกั่วในน้ำ รวมถึงสร้างแอปพลิเคชัน Kindly ที่ช่วยแก้ไขปัญหาการกลั่นแกล้งบนโลกไซเบอร์ (cyberbullying)
เธอเป็นคนที่สนใจวิทยาศาสตร์ตั้งแต่เด็ก ครั้นเธออายุได้ 10 ปี กิตันจาลี เรา ได้ยินข่าวเกี่ยวกับบวิกฤตการณ์น้ำฟลินต์ (Flint water crisis) ซึ่งเป็นวิกฤตด้านสาธารณสุขและสิ่งแวดล้อมที่เริ่มต้นในปี พ.ศ. 2557 เกิดการปนเปื้อนของสารตะกั่วในแหล่งน้ำ
นั่นจึงเป็นจุดเริ่มต้นทำให้เธอสนใจวิธีการวัดปริมาณสารตะกั่วในน้ำจนสามารถประดิษฐ์เครื่องตรวจวัดระดับตะกั่วในน้ำได้สำเร็จ เรียกว่า ‘Tethys’ โดยใช้ท่อนาโนคาร์บอน (carbon nanotubes) ที่ส่งข้อมูลคุณภาพน้ำผ่านบลูทูทได้ และยังได้รับความร่วมมือกับนักวิทยาศาสตร์จากบริษัท 3M
จนเมื่อปี พ.ศ. 2560 กิตันจาลี เรา ก็ได้รับรางวัล Discovery Education 3M Young Scientist Challenge และได้รับเงินรางวัลกว่า 25,000 ดอลลาร์สหรัฐ สําหรับการประดิษฐ์ของเธอ
เครื่องตรวจวัดระดับตะกั่วในน้ำ Tethys ประกอบด้วยแบตเตอรี่ขนาด 9 โวลต์ หน่วยตรวจจับตะกั่ว ส่วนต่อขยายบลูทูทและโพรเซสเซอร์
โดยสิ่งประดิษฐ์นี้ใช้ท่อนาโนคาร์บอนซึ่งค่าความต่างศักย์จะเปลี่ยนเมื่อมีการสัมผัสกับตะกั่ว เธอเรียนรู้เรื่องเกี่ยวกับท่อนาโนคาร์บอนนี้จากเว็บไซต์ของสถาบันเอ็มไอที และได้นําเสนอแนวคิดของเธอเองในการประชุม MAKERS ปี พ.ศ. 2561 จนสามารถระดมทุนได้อีก 25,000 ดอลลาร์สหรัฐ
นอกจากนี้ แอปพลิเคชันที่เธอพัฒนาชื่อว่า “Kindly” ซึ่งใช้ปัญญาประดิษฐ์ที่สามารถตรวจจับการกลั่นแกล้งทางอินเทอร์เน็ตได้ตั้งแต่ระยะแรก และได้ร่วมมือกับกองทุนเพื่อเด็กแห่งสหประชาชาติ (UNICEF) เพื่อเปิดตัวบริการทั่วโลก
จนกระทั่งในปี ปี พ.ศ. 2563 กิตันจาลี เรา ได้กลายเป็นบุคคลแรกที่ได้รับคัดเลือกให้เป็นเด็กแห่งปีจากนิตยสารไทม์ ด้วยวัยเพียง 15 ปี นับว่าเป็นอีกตัวอย่างหนึ่งของคนรุ่นใหม่ที่ลุกขึ้นมาเปลี่ยนแปลงสังคม
กิตันจาลี เรา ยังกล่าวอีกว่า เธอไม่เพียงแต่ต้องการสร้างอุปกรณ์เพื่อแก้ไขปัญหาที่โลกกำลังเผชิญอยู่ แต่เธอเองต้องการสร้างแรงบันดาลใจให้กับทุกคนก็สามารถทำได้เช่นกัน
ไม่ว่าการเสี่ยงโชคงวดนี้จะเป็นอย่างไร โปรดจำไว้ เราพร้อมมอบความรู้ใหม่ ๆ ให้คุณเสมอ แบบไม่ต้องรอโชคช่วย…
#แม้คุณจะไม่ถูกหวยแต่คุณจะรวยความรู้ #พบกันใหม่งวดหน้า
อ้างอิงจาก
- หนังสือของ James P. Sethna : https://sethna.lassp.cornell.edu/StatMech/EntropyOrderParametersComplexity20.pdf
- Complex system : https://en.wikipedia.org/wiki/Complex_system
- Lorenz system : https://en.wikipedia.org/wiki/Lorenz_system
- Gitanjali Rao https://workpointtoday.com/time-gitanjali-rao/