ฟิสิกส์กับการวาดรูปและฝันกลางวัน

เรื่องและภาพโดย ไอซี วริศา ใจดี

และแล้วฟิสิกส์กับการวาดรูปก็เดินทางมาถึงอีกมุมมองหนึ่งในการวิเคราะห์สถานการณ์ twin paradox นั่นคือการวาดแผนภาพ spacetime หรือการวาดกราฟตามตำแหน่งและเวลาของเหตุการณ์ ลงบนระบบพิกัดที่มีแกนแนวนอนเป็น space หรือตำแหน่ง และแกนแนวตั้งเป็น time หรือเวลานั่นเอง

นี่เป็นอีกหนึ่งเทคนิคในการวาดภาพจำลองปัญหาสุดงงให้ออกมาเข้าใจง่ายและสมเหตุสมผลโดยแทบไม่ต้องใช้การคำนวณ

อย่างที่ฉันได้เล่าไว้ในทฤษฎีสัมพัทธภาพฉบับก่อนหน้านี้ เราพบว่าเหตุการณ์ที่เกิดใน space และ time เมื่อมองจากกรอบอ้างอิงแต่ละกรอบที่ต่างกัน ค่าพิกัดทั้งสองนี้แตกต่างไปจากเดิมได้ แผนภาพ spacetime ประกอบไปด้วย แกนเวลา แกนตำแหน่ง เส้นโลก (world line) แสดงวิถีของวัตถุหนึ่ง ๆ ผ่านตำแหน่งและเวลา

หากเราลองวาดแผนภาพ spacetime ของสถานการณ์จรวดพุ่งผ่านดาวโลกไปด้วยความเร็ว v ในกรอบอ้างอิงดาวโลก จากรูปจะเห็นว่า เส้นโลกของดาวโลกนั้นมีลักษณะเป็นเส้นขนานไปกับแกนเวลาในแนวตั้งและตั้งฉากกับแกนตำแหน่งในแนวนอน แสดงถึงวัตถุที่หยุดนิ่งอยู่กับที่ เนื่องจากมันมีตำแหน่งที่คงที่ตลอดเวลา กล่าวคือ เส้นโลกของวัตถุที่อยู่นิ่งจะขนานไปกับแกนเวลานั่นเอง ในขณะเดียวกันเส้นโลกของจรวดที่กำลังวิ่งด้วยความเร็ว (ความเร็วเท่ากับระยะทางหารเวลาที่ใช้ในการเดินทางผ่านระยะทางนั้น ๆ) ตำแหน่งของจรวดจะเปลี่ยนไปตามเวลาที่เดินไป ทำให้เส้นโลกของจรวดมีลักษณะเอียงด้วยความชันเท่ากับ (แกนตั้งหารด้วยแกนนอน) หรือส่วนกลับของความเร็ว นั่นเอง นั่นแปลว่า หากเรารู้ความเร็วของวัตถุที่เราต้องการวาดแผนภาพ เราสามารถหาความชันของเส้นโลกของวัตถุนั้น ๆ ได้โดยความชันเท่ากับ

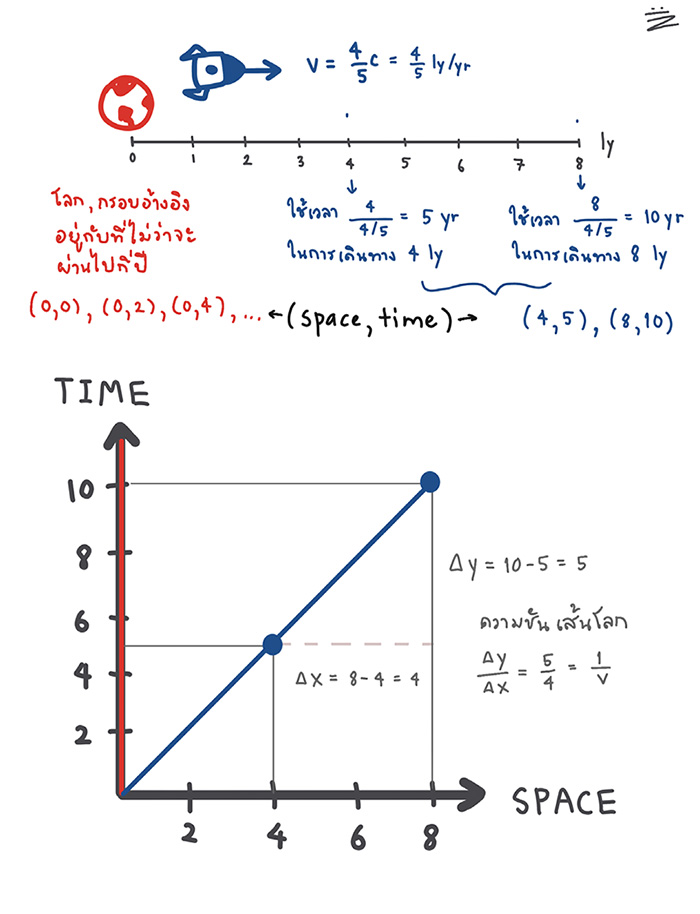
ถ้าเราวาดแผนภาพพวกนี้ดี ๆ บนกระดาษกราฟสเกลละเอียด เราก็สามารถแก้ปัญหาได้โดยไม่ต้องคำนวณด้วยสูตรอย่างคราวก่อน เจ๋งไหมล่ะ

เอาละ ทีนี้ลองกลับมาดูพาราด็อกซ์ฝาแฝดกัน ในกรณีนี้ความเร็วคือความเร็วแสง และเวลาคือปีแสง เมื่อคูณกันจะได้แกนตั้งที่มีหน่วยเป็นปีตามปกติ ส่วนแกนนอนคือ space หรือระยะทางมีหน่วยเป็นปีแสง กราฟที่วาดลงบนพิกัดสองแกนนี้เรียกว่า world line โดยความชันของเส้นกราฟจะมีค่าเท่ากับส่วนกลับของความเร็ววัตถุ

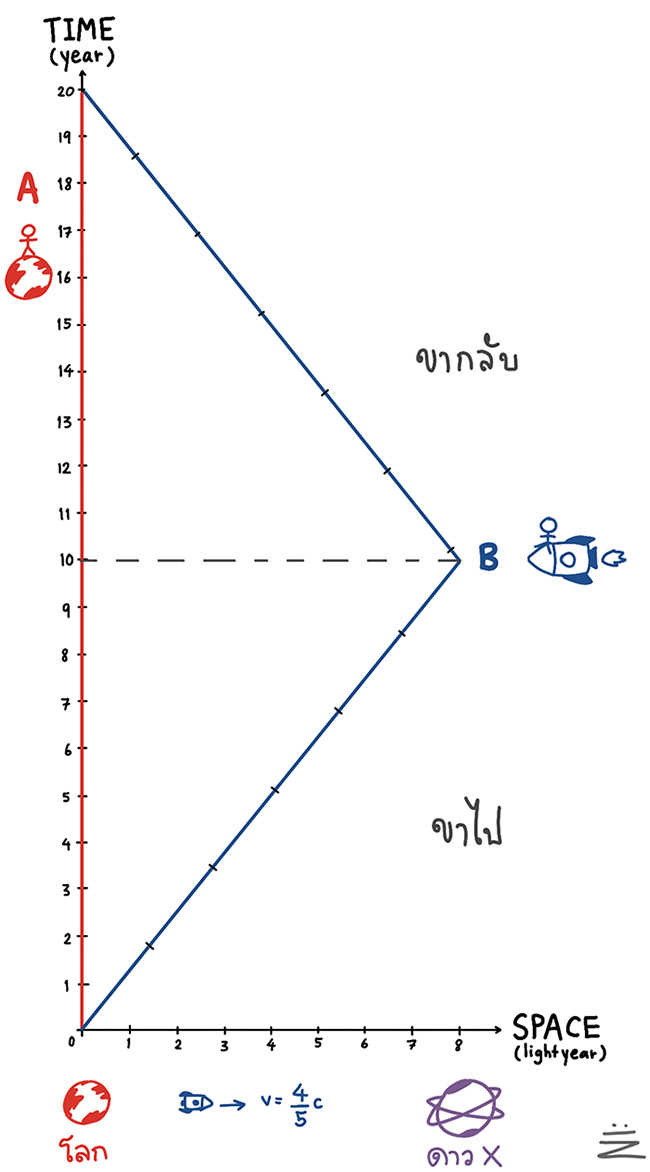
ภาพ Space-Time Diagram ในกรอบอ้างอิงของ A

ในภาพจะเห็นเส้นหนาสีแดงที่ขนานทับไปกับแกนแนวตั้ง คือ world line ของ A เนื่องจากเป็นกรอบอ้างอิงของ A แปลว่า A ไม่มีการเคลื่อนที่ ตำแหน่งของ A จึงอยู่ที่เดิม แต่เวลาของ A เดินต่อไปเรื่อย ๆ ตามแกนตั้ง ส่วนเส้นหนาสีน้ำเงินเป็น world line ของ B เป็นเส้นที่มีความชันเท่ากับ ก่อนจะเปลี่ยนเป็น – หรือว่าเคลื่อนที่วกกลับเมื่อถึงดาว X ที่ตำแหน่ง 8 ปีแสงนั่นเอง

ในที่นี้จะสังเกตได้ว่า บนเส้นโลกของ A แสดงเวลา 20 ปี ส่วนเส้นโลกของ B แสดงเวลาแค่ 12 ปี นั่นเพราะตามหลักสัมพัทธภาพแล้ว ในกรอบอ้างอิงของ B ที่จักรวาลรอบ ๆ ตัวเป็นฝ่ายเคลื่อนที่ผ่านจรวดไปด้วยความเร็ว จะทำให้เกิดการหดของระยะทาง จากที่ดาว X อยู่ห่างไป 8 ปีแสง ก็จะหดตามสมการ เหลือเป็น 4.8 ปีแสง รวมไปกลับแล้วก็ 9.6 ปีแสง ส่วน B ใช้เวลาเพียง = 12 ปี ในการเดินทางไปถึงดาว X

คราวนี้เราจะได้ใช้เสาหลักของสัมพัทธภาพที่ว่าความเร็วแสงคงที่ในทุกกรอบอ้างอิงให้เกิดประโยชน์ เพราะอย่างน้อยเราก็รู้แน่ชัดว่าแสงใช้เวลา 1 ปีในการเดินทางระยะ 1 ปีแสง โดยเราจะสมมติให้ A และ B ส่งสัญญาณแสงหากันทุกวันแรกของปี พร้อมบันทึกเวลาที่ได้รับสัญญาณจากอีกฝ่าย ทุก ๆ หนึ่งสัญญาณที่อีกฝ่ายได้รับเป็นการนับครบรอบ 1 ปีของผู้ส่ง นั่นทำให้ทั้งคู่ติดตามได้ว่าเวลาของอีกฝ่ายเดินช้าเร็วเป็นอย่างไรบ้าง ทั้ง A และ B จะพบว่าเวลาของอีกฝ่ายเดินเร็วขึ้นและช้าลงในสัดส่วนที่ต่างกันไปจากการสังเกตความถี่ของสัญญาณที่ส่งไปและได้รับมา ไปดูกันเลย

ในที่นี้จะเรียกสัญญาณว่าจดหมายฉบับที่ 1, 2, 3,… โดยสมมติว่าต่างฝ่ายต่างเขียนจดหมายอวยพรวันเกิดให้แก่กันนับจากวันเกิดปีที่ 20 ที่ฉลองพร้อมกันบนโลก และเส้นทางเดินของสัญญาณแสงนี้ระบุด้วยเส้นที่ทำมุม 45 องศากับแกนนอน เพราะตามนิยาม แสงใช้เวลา 1 ปีในการเดินทางไประยะ 1 ปีแสง

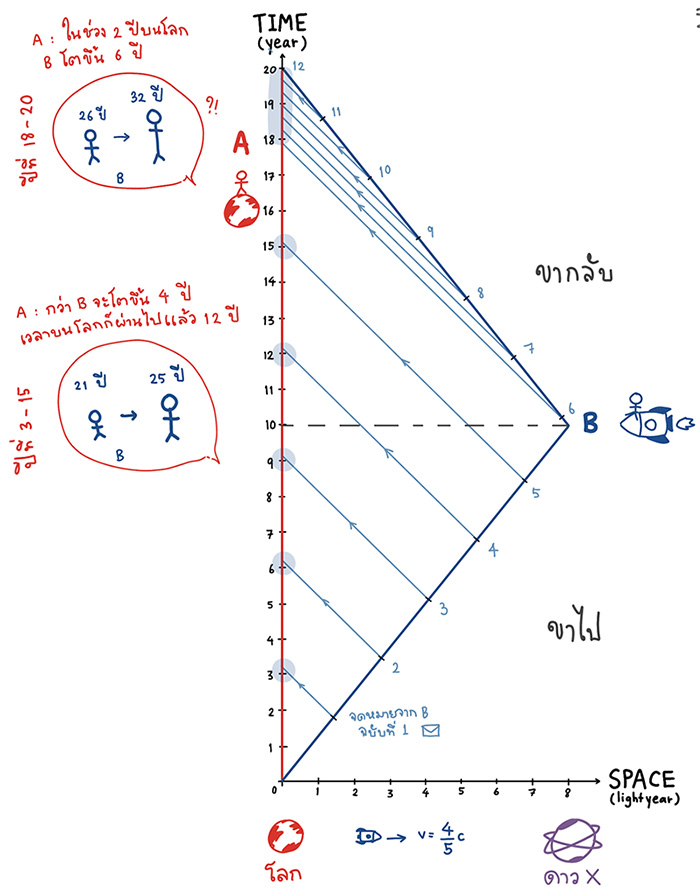
ภาพแสดงการเดินทางของจดหมายที่ A บนโลกได้รับจาก B

เมื่อลองกะดูคร่าว ๆ จากกราฟ ในขาเดินทางไปยังดาว X พบว่า กว่าจดหมายที่ A ส่งจากโลกจะเดินทางไปถึง B เวลาบนโลกก็ได้ผ่านไปแล้วประมาณ 5 ปี นับจากวันที่ B เริ่มออกเดินทางจากโลก แต่สำหรับ B แล้ว ในตอนที่ได้รับจดหมายจาก A นั้น เวลาของ B ได้ผ่านไปเพียง 3 ปีหลังจากโลกมา

เมื่ออีก 1 ปีบนโลกผ่านไป A ก็ได้กดส่งจดหมายฉบับที่ 2 ไปอีก เนื้อความอาจจะถามว่า “สุขสันต์วันเกิดปีที่ 22 เพิ่งจะผ่านไปสองปีเอง คงอีกนานเลยเนอะกว่าจะถึงดาว X” และแน่นอนว่ากว่าจดหมายนี้จะเดินทางไปถึง B ก็เป็นเอาตอนที่ B ได้ถึงดาว X และเตรียมยูเทิร์นยานกลับโลกพอดี

กลายเป็นว่าตลอดระยะเวลา 6 ปีของการเดินทางขาไปจนถึงดาว X ของ B เธอจะได้รับจดหมายเพียง 2 ฉบับจาก A แต่ในขากลับ กราฟที่เราวาดแสดงให้เห็นว่าจดหมายที่ A ส่งด้วยความถี่ปีละฉบับเหมือนเดิม กลับมาถึง B ถี่กว่าเก่า และในการเดินทางขากลับ ก่อนถึงโลก B ก็ได้รับจดหมายสุขสันต์วันเกิดที่เหลืออีก 17 ฉบับรัว ๆ เลย

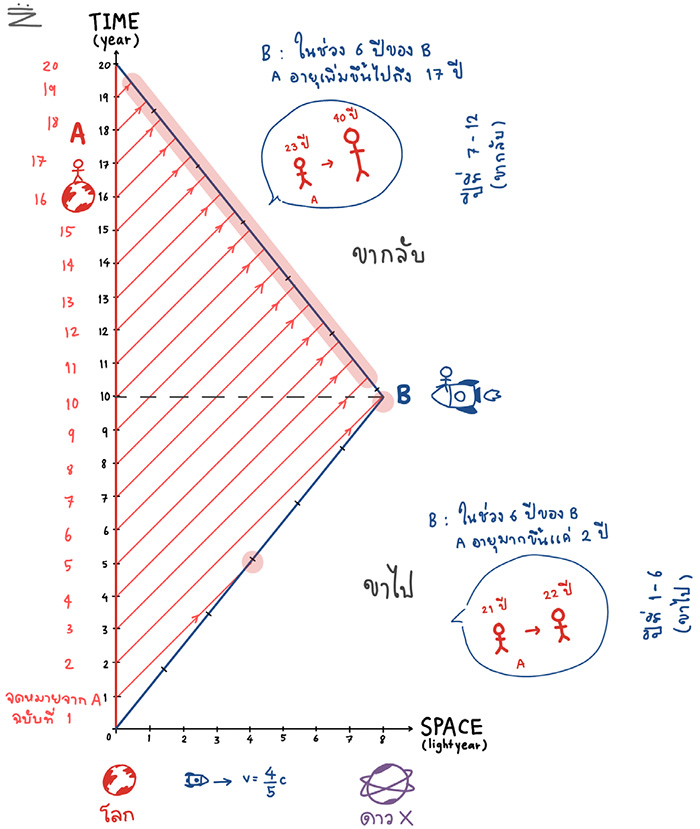
ภาพแสดงการเดินทางของจดหมายที่ B ได้รับจาก A บนโลก

คราวนี้มาดูจดหมายของ B กันบ้าง ในปีแรกของการเดินทาง B ได้ส่งจดหมายหา A แต่กว่าจดหมาย “สุขสันต์วันเกิดปีที่ 21” จะไปถึง A ที่อยู่บนโลกนั้น เวลาได้ผ่านไปกว่า 3 ปี A ก็อายุ 23 ไปแล้ว และจดหมายอีก 4 ฉบับที่ B ส่งระหว่างการเดินทางขาไปก็เป็นเช่นเดียวกัน จนกระทั่ง B เดินทางถึงดาว X และเริ่มวกกลับโลก ในตอนนั้นเองจดหมายฉบับที่ 6 ของ B ที่เขียนว่า “สุขสันต์วันเกิดปีที่ 26 เริ่มเดินทางกลับแล้ว ไว้เจอกัน !” ก็เดินทางมาถึงในตอนที่ A อายุ 38 ไป เอาละ เราคงจะว่าอะไรไม่ได้ที่ B ดูจะส่งจดหมายล่าช้าไปเยอะเลย แต่ระหว่างขากลับของ B จดหมายที่มาถึง A ถี่ขึ้นก็ดูจะเป็นข้อแก้ตัวที่ดีได้ ในท้ายที่สุดแล้วจดหมายฉบับที่ 11 หรือฉบับสุดท้ายของ B ก่อนถึงโลก ที่เขียนว่า “สุขสันต์วันเกิดปีที่ 20+11=31 ! ใกล้ถึงโลกแล้วเย้…” ก็เดินทางมาถึง A ก่อนวันเกิดปีที่ 40 ของ A นิดเดียว และเมื่อทั้งคู่กลับมาเจอกันอีกครั้ง B ก็มีอายุ 32 (20+12) ปี ในขณะที่ A มีอายุ 40 (20+20) ปี ตรงกับการคำนวณที่เราเคยทำกันไปในฉบับที่แล้ว

จากทั้งสองเหตุการณ์ที่เกิดควบคู่กัน ถ้าเราให้แฝดแต่ละคนบันทึกเวลาที่จดหมายมาถึงเป็นตัวบ่งชี้อายุของอีกฝ่าย B จะพบว่า ในขากลับเขาจะได้รับสัญญาณจาก A ถี่กว่าขาไป หรือก็คือในช่วง 6 ปีที่ B เดินทางขาไป A จะมีอายุเพิ่มขึ้นด้วยอัตราที่ช้าลง ก่อนเร่งเร็วขึ้นในช่วง 6 ปีจรวดสุดท้ายที่ B เดินทางขากลับ แปลว่าในมุมมองของ B อายุของ A เพิ่มเร็วขึ้นในช่วง 50 เปอร์เซ็นต์ และช้าลง 50 เปอร์เซ็นต์ (ของ 12 ปีจรวด) เป็นสัดส่วนเท่า ๆ กันอย่างละ 6 ปีจรวด

ส่วน A ที่อยู่บนโลกจะพบว่าในช่วง 18 ปีโลก หรือกว่า 90 เปอร์เซ็นต์ของเวลา 20 ปีโลกที่ทั้งคู่จากกันนั้น เวลาของ B ช้าลง กล่าวคือ A พบว่า B อายุเพิ่มขึ้นในอัตราที่ช้าลงกว่าปกติ ส่วนอีก 10 เปอร์เซ็นต์สุดท้ายที่เหลือก่อน B เดินทางกลับถึงโลก อายุของ B ก็กลับมาเพิ่มเร็วขึ้น

โดยรวมแล้วจากคำกล่าวของทั้งสอง อายุของ A มีสัดส่วนของช่วงที่เดินเร็วขึ้นถึง 50 เปอร์เซ็นต์ ส่วน B มีสัดส่วนของช่วงที่เดินเร็วขึ้นเพียง 10 เปอร์เซ็นต์ และนั่นเห็นพ้องต้องกันกับข้อสรุปที่ว่า เมื่อทั้งคู่กลับมาเจอกันอีกครั้งบนโลก A จะมีอายุมากกว่า B นั่นเอง

จะเห็นได้ว่า การวาดกราฟทำให้แทบจะไม่ต้องคำนวณเลย

ด้วยการคำนวณผสมวาดรูปนี้ ผลจากทั้งสองกรอบอ้างอิงจึงเห็นพ้องต้องกันได้ และแล้วพาราด็อกซ์ก็คลี่คลายในที่สุด !

ขอขอบคุณศาสตราจารย์ James Battat แห่ง Wellesley College ผู้สอนวิชาฟิสิกส์ เรื่องทฤษฎีสัมพัทธภาพพิเศษ