เล่นสนุกชวนฉุกคิดกับ Tuckerman Traverse

เรื่องและภาพโดย ไอซี วริศา ใจดี

วันนี้เราจะมาไขปริศนาที่ฉันได้ทิ้งท้ายไว้ในฉบับที่แล้วกัน ! หลังจากที่ฉันใช้ความพยายามลองสลับรูปแบบการเปิดดูอีกครั้ง ด้วยการพลิกเจ้าเฟล็กซากอนกลับไปกลับมา ในที่สุดเลข 6 ก็ปรากฏตัวขึ้นมา

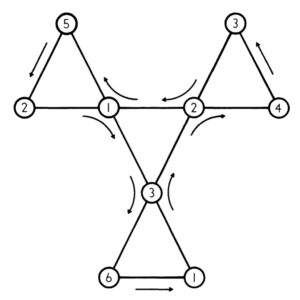
ในครั้งนี้ฉันเริ่มเปิดจากหน้าเลข 2 เหมือนเดิม เมื่อเปิดออกจะได้เลข 3 ซึ่งฉันพบว่าหน้าเลข 3 สามารถเปิดได้สองมุม มุมหนึ่งจะพาเราวกกลับวงจรเดิมคือกลับไปเลข 4 และตามด้วยเลข 2 อีกครั้ง แต่อีกมุมหนึ่ง เมื่อเปิดออกมาจะพบกับเลข 1 และตามมาด้วยเลขที่เราตามหาก็คือ…เลข 6 นั่นเอง ! เมื่อจบลงที่เลข 6 เราจะพบว่าสามารถเปิดได้แค่มุมเดียวที่นำเรากลับมายังเลข 3 เป็นวงจรในรูปแบบ 3>1>6 ดังภาพประกอบที่ 1

ภาพประกอบที่ 1 ลำดับการเปลี่ยนหน้าของเฮกซะเฮกซะเฟล็กซากอนแบบ 3>1>6

มาถึงตรงนี้เกิดคำถามขึ้นในใจฉันว่า ถ้าหากว่าเฟล็กซากอนมีมากกว่า 6 หน้าขึ้นมาล่ะ ฉันจะนั่งวนเปิดได้ครบหมดทุกหน้าไหม และในฉบับนี้ ฉันมีคำตอบ !

ก่อนอื่นเรามาทำความรู้จักบุคคลสำคัญอีกท่าน ผู้เป็นหนึ่งในการร่วมก่อตั้งสมาคมเฟล็กซากอน ซึ่งเป็นเพื่อนของคุณสโตน และเป็นนักศึกษาสาขาคณิตศาสตร์ ชื่อคุณไบรอันท์ ทักเคอร์แมน (Bryant Tuckerman) จากความสงสัยที่ว่าทำไมเลข 6 ถึงไม่ค่อยปรากฏมาให้เห็นเลยด้วยวิธีการพลิกแบบซ้ำๆ ในรูปแบบเดิม คุณทักเคอร์แมนได้อธิบายรูปแบบการเปลี่ยนหน้าของเฮกซะเฮกซะเฟล็กซากอนแบบ 6 หน้า โดยใช้การวาดแผนผังเข้ามาช่วย หลักการของเขาก็คือ เปิดที่มุมเดิมต่อๆ กันจนกระทั่งได้หน้าที่เปิดได้แค่มุมเดียว

เทคนิคนี้เรียกว่า ทักเคอร์แมนทราเวิร์ส (Tuckerman Traverse) เมื่อเปิดไปเรื่อยๆ ก็จะพบแบบรูปที่วนไปมาอยู่ 3 หน้าซ้ำๆ

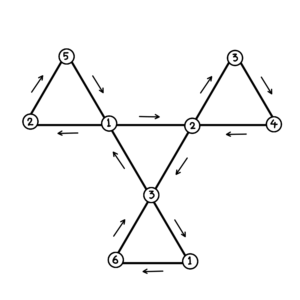
เขาจึงนำมาวาดเป็นวงจรสามเหลี่ยมที่ประกอบด้วยตัวเลขทั้งสาม ได้แก่ วงจร 5,2,1 วงจร 1,3,2 วงจร 3,6,1 และวงจร 2,4,3 ก่อนจะเชื่อมโยงวงจรทั้งสี่เข้าด้วยกัน จนเกิดเป็นเส้นทางที่มีรูปแบบ (pattern) แน่ชัด หากใครเปิดเฟล็กซากอนตามลำดับนี้ก็จะพบครบทั้ง 6 หน้าแน่ๆ ดังภาพประกอบที่ 2

ภาพประกอบที่ 2 แสดงแผนผัง Tuckerman Traverse แบบต้นฉบับจากหนังสือ* (ซ้าย) กับแบบกลับด้านที่ตรงกับการทดลองเปิดของฉัน (ขวา)

แผนผังของคุณทักเคอร์แมนดังรูปซ้ายนี้ใช้ได้ทั้งด้านหน้าและด้านหลังของเฟล็กซากอน วงจรจะยังคงเหมือนเดิมเพียงแต่ลำดับที่ได้จะย้อนกลับ แค่สลับหัวลูกศรไปในทิศตรงข้าม จะเห็นว่าลำดับของคุณทักเคอร์แมนเป็น 6>1>3 แต่ของฉันเป็น 3>1>6 ทำให้รู้ว่า ฉันได้เริ่มเล่นเฟล็กซากอนจากด้านตรงกันข้ามกับคุณทักเคอร์แมน

ด้วยแผนผังทักเคอร์แมน เราสามารถเปิดครบทั้ง 6 หน้า และใช้ขั้นตอนน้อยที่สุด โดยเราเลี่ยงไม่ได้ที่จะเจอเลข 1,2,3 ซ้ำถึงเลขละ 3 ครั้ง แต่เลข 4,5,6 จะโผล่มาให้เห็นเพียงเลขละครั้งเดียว สรุปรวมจำนวนครั้งการเปิดน้อยที่สุดคือ 3+3+3+1+1+1= 12 ครั้งเท่านั้นเอง

นอกจากนี้ ยังใช้แผนผังนี้ได้กับเฮกซะเฟล็กซากอนทุกรูปแบบ ถ้าเราทดลองใช้กับ ไตรเฮกซะเฟล็กซากอนที่มีแค่ 3 หน้า ก็ดูแค่สามเหลี่ยมใจกลางของแผนผัง ส่วนในกรณีเฮกซะเฟล็กซากอนที่มีจำนวนหน้ามากกว่า 6 ขึ้นไป จากการคำนวณต่อจากแผนผัง คุณทักเคอร์แมนและผองเพื่อนสมาคมเฟล็กซากอนพบว่า โดยเชิงทฤษฎีแล้ว เฟล็กซากอนสามารถมีหน้าได้มากถึง 9,12,15,.. หรือมากกว่านั้นอีก โดยการเพิ่มจำนวนสามเหลี่ยมลงไปในแถบกระดาษให้ยาวขึ้นเรื่อยๆ ไม่มีสิ้นสุด แต่ตามหลักความจริงจะทำออกมาได้ไหมนั้นก็อยู่ที่ความยาวของกระดาษ และความสามารถในการพับกระดาษทับซ้อนกัน ซึ่งสถิติที่คุณทักเคอร์แมนเคยทำได้จริงนั้นสามารถเปลี่ยนได้ถึง 48 หน้าแน่ะ !

ต่อมาในปี พ.ศ. 2483 คุณทักเคอร์แมนและคุณไฟยน์แมน ได้ทำการสรุปทฤษฎีเฟล็กซากอนฉบับสมบูรณ์ขึ้น เพื่ออธิบายวิธีสร้างเฟล็กซากอนที่ครอบคลุมการสร้างเฟล็กซากอนรูปแบบต่างๆ รวมถึงระบุคุณสมบัติและความยาวของกระดาษที่ต้องใช้ และเพิ่มเทคนิคแหวกแนวอย่างการใช้กรรไกรซิกแซ็กเข้ามาช่วยตัดเพื่อสร้างรูปร่างใหม่ๆ ถึงแม้จะไม่ได้ตีพิมพ์ออกมา แต่ผลงานของเขาทั้งสองกลายเป็นแรงบันดาลใจให้นักคณิตศาสตร์รุ่นใหม่มานั่งพับกระดาษเล่นเพื่อศึกษาและมุ่งต่อยอดทฤษฎีของพวกเขากันต่อ

น่าทึ่งใช่ไหมล่ะว่าภายในของเล่นชิ้นแบนๆ นี้จะอัดแน่นด้วยรูปแบบที่ต่างกัน แถมยังอัดแน่นด้วยความรู้ที่โยงใยไปสู่ทฤษฎีทางวิชาการอีกด้วย ! และ…ยังไม่จบเพียงแค่นั้น

แน่นอนว่าความนิยมเฟล็กซากอนที่แพร่หลายนั้นไม่จำกัดเพียงในหมู่นักคณิตศาสตร์ ใครหลายๆ คนที่ได้ลองเล่นแล้วก็อดไม่ได้ที่มีอารมณ์ศิลปิน ลองตกแต่งเฟล็กซากอนกันเสียหน่อย ฉันเองก็ได้ทดลองวาดรูปการ์ตูนน่ารักๆ ลงไป พอเริ่มพลิกเล่นไปเรื่อยๆ ฉันก็พบกับเรื่องไม่คาดฝันเข้า ! เห็นอะไรแปลกๆ กันไหม ? เราสามารถเปิดได้หน้าเดิมทุกครั้งรึเปล่า หรือว่ารูปแบบการจัดเรียงมันเปลี่ยนไปนะ ?

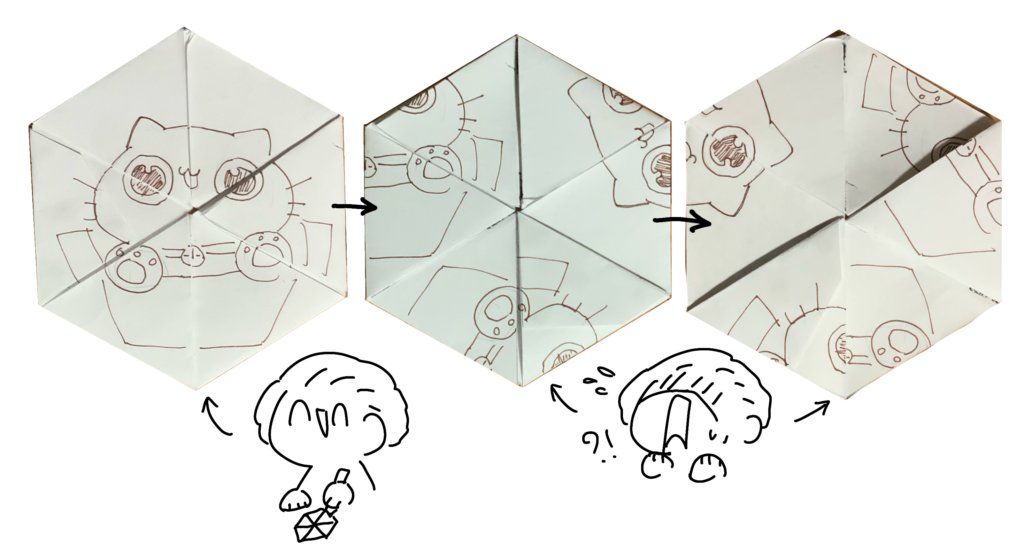
ภาพประกอบที่ 3 เฮกซะเฮกซะเฟล็กซากอนที่ฉันวาดรูปลงไป กับตอนที่พลิกเปลี่ยนหน้าแล้วพบว่าภาพที่วาดไว้สวยๆ กลับแยกชิ้นส่วนไปคนละทิศละทางกันซะได้

เอาละ ฉันรู้อยู่ว่าเฮกซะเฮกซะเฟล็กซากอนนั้นเปิดได้ 6 หน้าที่แตกต่างกันไป แต่คราวนี้ในหน้าเดียว ฉันกลับได้แบบรูปที่ต่างกันออกไปถึงสาม ?! ทำไมพอพลิกแล้วรูปวาดบนเฟล็กซากอนของฉันเละเทะไปล่ะ เฟล็กซากอนของฉันพังหรือเปล่า ? มันเกิดอะไรขึ้นกันแน่ ?!

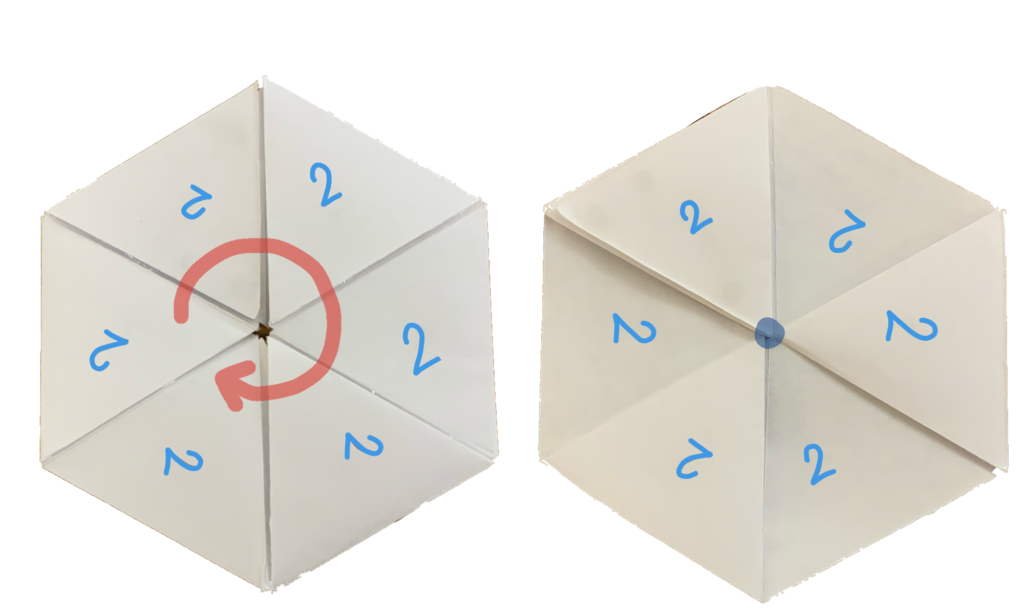
ใครสังเกตได้ฉันขอปรบมือให้ ถูกต้อง ! จริงๆ เหตุการณ์นี้เกิดขึ้นมาแล้ว ! แต่ฉันมองข้ามไปเพราะตัวเลขที่เรียงกันมันไม่ชัดเจนเท่าตอนที่วาดรูป ตอนแรกฉันเขียนตัวเลขลงในแต่ละหน้าของเฮกซะเฮกซะเฟล็กซากอนโดยเรียงทิศทางของตัวเลขแบบตามเข็มนาฬิกา ดังภาพประกอบที่ 4 (ซ้าย) พอลองดูดีๆ บางครั้งที่เปิดออกมา กลับพบว่าตัวเลขเรียงแบบหันเข้าหาศูนย์กลางแทน ดังภาพประกอบที่ 4 (ขวา)

ดังนั้นเมื่อวาดรูปลงไปแล้วพลิกดู จึงสังเกตเห็นได้ชัดเจนขึ้นว่ารูปที่วาดไว้นั้นไม่ปะติดปะต่อกัน กลายเป็นเละเทะไปเสียหมด ฉันจึงรู้ว่าในหน้าหนึ่งๆ ของเฮกซะเฮกซะเฟล็กซากอนปรากฏได้สองรูปแบบที่แตกต่างกัน แต่ปัญหาคือเฟล็กซากอนของฉันติดกาวไว้เรียบร้อยแล้ว แล้วทำไมสามเหลี่ยมถึงไม่ยึดอยู่กับที่เดิมของมันล่ะ ?! มันขยับเปลี่ยนไปได้ยังไงกัน ?!

ภาพประกอบที่ 4 การจัดเรียงของเลข 2 ที่ต่างกันในการพลิกแต่ละครั้ง

แสดงว่ากุญแจสำคัญของการที่หน้าเฟล็กซากอนจะประกอบกลับเป็นรูปเดิมได้อยู่ที่มุมและด้านที่มาประกบกัน และเฮกซะเฟล็กซากอนที่เป็นรูปหกเหลี่ยนด้านเท่าก็ประกอบไปด้วยสามเหลี่ยมด้านเท่าที่หันมุมยอดเข้าหากัน ภาพที่ปรากฏแตกต่างกันทำให้เรารู้ว่าระหว่างการพับแล้วพลิกเฟล็กซากอนไม่เพียงแต่เปลี่ยนหน้า แต่มีการหมุนของสามเหลี่ยมเกิดขึ้นด้วย !

เมื่อรู้เช่นนี้แล้ว นักคณิตศาสตร์ก็อดไม่ได้ที่จะนึกหาวิธีมาอธิบายปรากฏการณ์นี้ เมื่อรูปบนหน้าเฟล็กซากอนไม่ได้มีแค่ตัวเลขหรือสีเรียบๆ แต่กลับเป็นรูปเรขาคณิตที่ต่างกันอย่าง ฉันได้ทดลองวาดรูปสัญลักษณ์ ดาวหกแฉก วงกลม และหกเหลี่ยมลงไปตามมุมของเฮกซะเฮกซะเฟล็กซากอน โดยอ้างอิงมาจากหนังสือ Hexaflexagons ของคุณมาร์ติน การ์ดเนอร์ พอพลิกดูก็พบว่าได้ผลดังภาพประกอบที่ 5

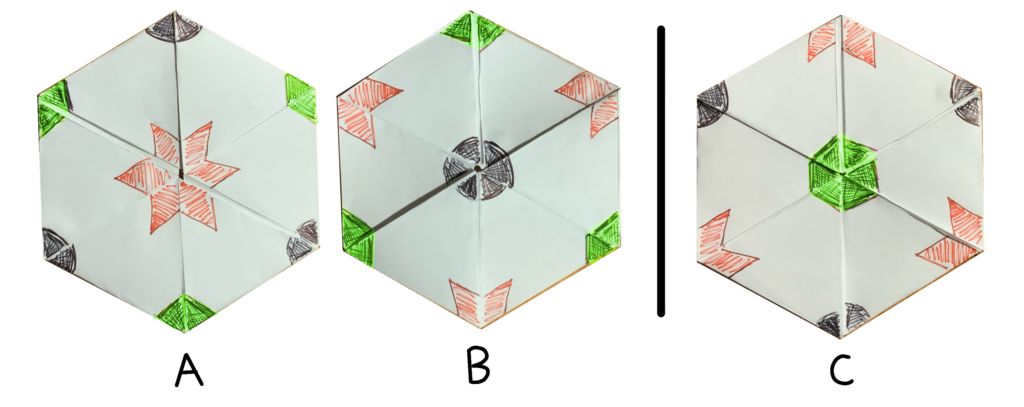
ภาพประกอบที่ 5 การเปลี่ยนแปลงของรูปที่วาดลงบนมุมทั้งสามของแต่ละสามเหลี่ยมที่ประกอบกันเป็นเฮกซะเฮกซะเฟล็กซากอน โดยทั้งสามภาพเป็นรูปแบบภายในหน้าหนึ่งๆ เท่านั้น ภาพ A, B เป็นภาพที่เกิดจากการเปิดแบบปกติ ส่วน C จะเกิดได้เมื่อพลิกกลับไปด้านหลัง

จากตรงนี้เราก็พอจะรู้ว่าในเฮกซะเฮกซะเฟล็กซากอนอันหนึ่ง แต่ละหน้าจะสามารถเกิดภาพได้ถึง 3 รูปแบบ เมื่อมันมี 6 หน้า เราจึงเจอรูปแบบการจัดเรียงที่แตกต่างกันไปถึง 18 รูปแบบเลยละ !

นับเป็นอีกเรื่องราวสนุกๆ ที่แสดงให้เห็นว่า เรื่องราวของตัวเลขสามารถพบเจอได้ทั่วไปในชีวิตประจำวันของผู้คน ไม่เว้นแม้แต่ในของเล่นจากกระดาษพับที่ดูแสนจะธรรมดา หลักการทางคณิตศาสตร์ได้เข้ามาช่วยอธิบายไขข้อสงสัย และนำพาเราไปสู่ความรู้ในรูปแบบใหม่ๆ ที่ได้ทั้งความสนุก แถมยังได้เรียนรู้กระบวนการคิดเชิงคณิตศาสตร์ด้วย นับเป็นรูปแบบการเรียนรู้ที่ผสมผสานหลักวิชาการเข้ากับศิลปะการเล่นได้อย่างกลมกลืน

ความลับของเฟล็กซากอนมีไม่สิ้นสุด เช่นเดียวกับจินตนาการของเหล่านักเฟล็กซ์ (flexigators) ทั้งหลาย รวมถึงฉันและผู้อ่านที่ได้ไปลองทำด้วย ไม่แน่เราอาจจะค้นพบทฤษฎีใหม่ๆ ก็เป็นได้

และเช่นเคยก่อนจะจบ ฉันอดไม่ได้ที่จะถามคำถามที่คุ้นเคยว่า “ใครได้ทดลองทำเล่นกันแล้วบ้าง”

สามารถส่งภาพมาให้ดูกันได้ที่เพจนิตยสารสาระวิทย์นะคะ มาดูกันว่าแต่ละคนจะวาดตกแต่งเป็นรูปอะไรกันบ้าง หรือใครนึกสนุกอยากจะลองทำลายสถิติ 48 หน้าของคุณทักเคอร์แมนได้ก็ลองดู !

เฟล็กซ์ให้สนุก แล้วเจอกันฉบับหน้านะคะ !

ขอบคุณข้อมูลจาก:

หนังสือ Hexaflexagons and Other Mathematical Diversions: The First ‘Scientific American’ Book of Puzzles and Games โดยคุณ Martin Gardner
Vihart – ช่องยูทูบของคุณ Vi Hart นักคณิตศาสตร์ชาวอเมริกัน