พาราด็อกซ์ฝาแฝด

เรื่องและภาพโดย ไอซี วริศา ใจดี

สาระวิทย์ในศิลป์ฉบับที่ผ่านมา ฉันได้พูดถึงเรื่องสัมพัทธภาพพิเศษไปแล้ว ในฉบับนี้ฉันขอนำเสนอตัวเอกใหม่ที่มีชื่อว่า “พาราด็อกซ์ฝาแฝด” หรือ “Twin Paradox” ปัญหาสุดโด่งดังที่ทำเอานักวิชาการหลายคนในอดีตถึงกับหัวหมุน

พาราด็อกซ์ฝาแฝดเป็นการทดลองทางความคิดที่ว่า หากเรามีฝาแฝดคู่หนึ่งสมมติว่าชื่อ A และ B โดยขณะที่ A อยู่บนโลก B ขึ้นจรวดไปท่องอวกาศ หลัง B เดินทางอยู่พักหนึ่งแล้วกลับมายังโลก ถ้าดูตามหลักการยืดของเวลา (time dilation) ในสัมพัทธภาพพิเศษ จะพบว่าเวลาของทั้งคู่จะเดินไม่เท่ากัน โดยเวลาของคนที่เคลื่อนที่จะเดินช้ากว่าของคนที่อยู่นิ่ง ส่งผลให้เมื่อ B เดินทางกลับมาถึงโลก A และ B จะไม่ได้เป็นฝาแฝดที่มีอายุเท่ากันอีกต่อไป

ปัญหาในที่นี้ก็คือต่างคนต่างพบว่าอีกฝ่ายนั้นอายุน้อยกว่าตนเอง ?! เพราะในมุมมองของ A ที่อยู่บนโลก คนที่เคลื่อนที่คือ B ที่อยู่ในจรวด A จึงเห็นว่า B มีอายุน้อยกว่า ในทางกลับกัน B ที่อยู่ในจรวดจะมองเห็นว่าคนที่เคลื่อนที่คือ A บนโลก B จึงเห็นว่า A ต่างหากที่เด็กกว่า

สรุปแล้วใครกันแน่ที่เด็กกว่านะ ?

อย่างไรก็ตาม ฉันขอบอกก่อนว่านี่มันไม่ใช่พาราด็อกซ์จริง ๆ หรอก หากแต่เป็นความเข้าใจผิดในสัมพัทธภาพพิเศษ ที่เราอธิบายได้ด้วยการใช้สมการ 3 สมการที่ฉันเคยบอกไว้ในสาระวิทย์ฉบับก่อนหน้านี้

เอาละ เราลองมาวิเคราะห์สถานการณ์ดูดี ๆ อีกครั้ง ! และเรียบเรียงข้อมูลกันใหม่ด้วยการคิดรวมตัวเลขเข้าไปเพื่อให้คำนวณต่อได้

เรื่องมีอยู่ว่า A และ B เป็นฝาแฝดอายุเท่ากัน ตอนที่ทั้งคู่มีอายุ 20 ปีบริบรูณ์ B ได้ออกเดินทางไกลไปยังดาว X ที่ห่างจากโลกเป็นระยะ 8 ปีแสง

โดยจรวดของ B เคลื่อนที่ด้วยความเร็วเท่ากับ 0.8 เท่าของความเร็วแสง (c) และเมื่อถึงดาว X ปุ๊บ B จะยูเทิร์นจรวดเพื่อเดินทางกลับสู่โลกทันที (เวลาในการกลับจรวดให้สมมติว่าเร็วมากจนไม่นับ) ทั้ง A และ Bได้เฝ้ารอวันที่จะกลับมาพบกันอีกครั้ง คำถามก็คือ เมื่อ B กลับถึงโลก เวลาของทั้งคู่จะต่างกันยังไงนะ

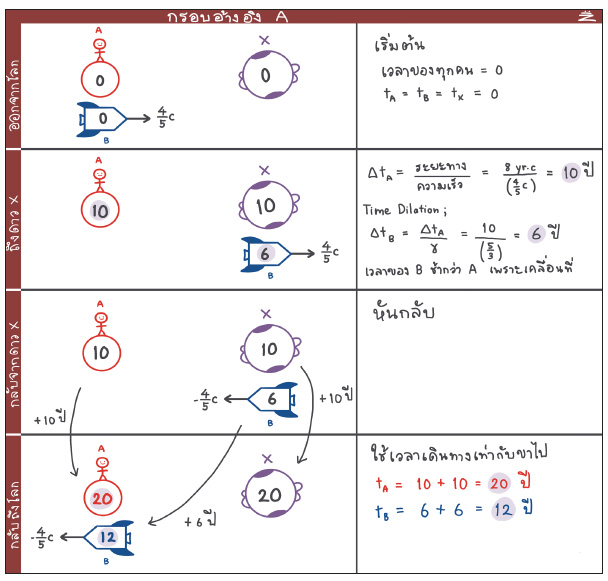
อย่างแรก ในกรอบอ้างอิงของ A สิ่งที่ A บนโลก คำนวณได้คือ ระยะเวลาจากวันที่ B เริ่มเดินทาง ถึงวันที่ B ไปถึงดาว X ที่ห่างออกไป 8 ปีแสง เมื่อนำระยะทางหารด้วยความเร็วจรวด A จะพบว่าอีก 10 ปี B จะถึงดาว X และอีก 10 ปีจึงจะกลับมายังโลก อย่างไรก็ตาม เนื่องจาก B กำลังเคลื่อนที่ นาฬิกาบนจรวดจึงเดินทางช้าลง โดยหาได้จากสูตร

นั่นแปลว่าเมื่อ B ถึงดาว X เขาจะรับรู้ว่าเวลาได้เดินไปเพียง 6 ปี และในขากลับก็เช่นเดียวกัน รวมแล้วทริปการเดินทางไป-กลับนี้ เวลาของ B เดินไปทั้งสิ้น 12 ปี แต่สำหรับ A เวลาบนโลกนั้นเดินไปแล้วถึง 20 ปี ทำให้เมื่อทั้งคู่มาเจอกันอีกครั้ง A จะแก่กว่า B อยู่ 8 ปีนั่นเอง

การคำนวณในกรอบอ้างอิง A ดังรูป

ในทางกลับกัน ถ้าเราคิดปัญหานี้ในกรอบอ้างอิงของ B ที่ A กลับกลายเป็นคนเคลื่อนที่ออกห่างจาก B เอง เราอาจจะไม่อยากคิดต่อเพราะมันก็น่าจะเหมือนเดิมแค่กลับกันไม่ใช่เหรอ โดย B ซึ่งตอนนี้หยุดนิ่ง จะแก่กว่า A ซึ่งตอนนี้กำลังเคลื่อนที่อยู่ 8 ปีเท่ากัน

แต่มันไม่ใช่แค่นั้น และตรงจุดนี้แหละที่ถูกเข้าใจผิดว่าเป็นพาราด็อกซ์ เพราะความเห็นของ A กับ B ดันไม่ตรงกันซะนี่ ต้องมาลองคำนวณดี ๆ เพื่อตัดสินว่าใครกันแน่ที่ถูก และใครกันแน่ที่แก่กว่ากัน

การคำนวณในกรอบอ้างอิง B ดังรูป

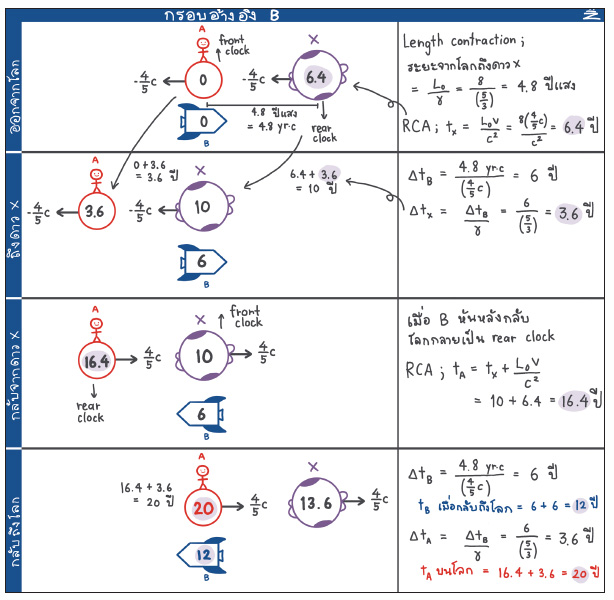
จะเห็นว่าได้ผลลัพธ์เหมือนกับการคำนวณในกรอบอ้างอิงของ A บนโลก และพาราด็อกซ์ก็คลี่คลายแล้ว ! ทั้งนี้เพราะ A นับเป็นกรอบอ้างอิงที่ไม่มีความเร่ง ส่วนของ B นั้นไม่ใช่ เพราะ B มีการหันวกกลับสู่โลก การเปลี่ยนทิศทางก็นับเป็นการเปลี่ยนแปลงการเคลื่อนที่ที่ก่อให้เกิดความเร่ง ทำให้ B ไม่ใช่กรอบอ้างอิงเฉื่อยอีกต่อไป และถ้าเราเผลอไปคิดวิเคราะห์สถานการณ์ตามเดิมก็จะใช้ไม่ได้ผล

ตอนที่ B หันหลังกลับ ยังนับเป็นจุดสำคัญในแง่การคำนวณอีกด้วย เพราะโลกกับดาว X กลับตำแหน่งกัน โลกกลายมาเป็น rear clock แทน (โลกเดินทางมาถึง B ทีหลัง) ทำให้ต้องปรับเวลาใหม่เพื่อให้ตรงตามหลักคำนวณข้อ 3 ที่ว่า นาฬิกาด้านหลังเดินเร็วกว่าด้านหน้า (RCA) โดยสรุปแล้ว เมื่อ B วกกลับมาถึงโลก A และทุกคนบนโลกจะแก่กว่า B เป็นเวลา 8 ปีจริง ๆ

อาจจะฟังดูเหลือเชื่อ แต่มีการทดลองที่พิสูจน์สำเร็จแล้วว่าเหตุการณ์เช่นนี้เกิดขึ้นได้จริง ฉันจะมาเล่าให้ฟังต่อในฉบับหน้า พร้อมวิธีมองปัญหานี้โดยการวาด Spacetime Diagram แทนการคำนวณ รอติดตามกันต่อได้เลย !