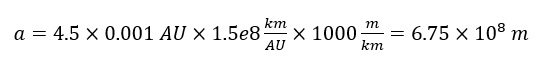เรื่องและภาพโดย ไอซี วริศา ใจดี
สาระวิทย์ฉบับนี้ ฉันจะชวนเพื่อน ๆ มาลองวัดมวลของดาวพฤหัสบดีด้วยการสังเกตการโคจรของดวงจันทร์รอบดาวพฤหัสบดี เราจะทำโดยใช้กฎของเคปเลอร์และการสังเกตจากบนโลกผ่านซอฟต์แวร์ Stellarium ที่จำลองท้องฟ้ายามค่ำคืนแบบเสมือนจริงแทนการอดนอนเพื่อเฝ้าดูดาวทุกคืน
อย่างที่เรารู้กันว่ากฎของเคปเลอร์เชื่อมโยงรอบการโคจรของดวงดาวเข้ากับน้ำหนักของวัตถุที่โคจรรอบมัน เราจึงใช้ความสัมพันธ์จากกฎนี้หาน้ำหนักของดาวพฤหัสบดีจากวงโคจรของดวงจันทร์บริวารของมันได้ และจากการสังเกตตำแหน่งที่เปลี่ยนไปในแต่ละช่วงเวลาของดวงจันทร์ จะทำให้เราประมาณค่าคร่าว ๆ ได้ว่า ดวงจันทร์ใช้เวลานานเท่าไหร่ในการโคจรรอบดาวพฤหัสบดีครบ 1 รอบ
เอาละมาเริ่มกันเลย… จากข้อมูลล่าสุดในปี พ.ศ. 2566 นี้ พบว่าดาวพฤหัสมีดวงจันทร์เป็นบริวารมากถึงกว่า 90 ดวง แต่ดวงหลัก ๆ ที่มีขนาดใหญ่และมองเห็นได้อย่างชัดเจนจากโลกเรามีด้วยกัน 4 ดวง คือ ไอโอ ยูโรปา แกนีมีด และคัลลิสโต ที่เรียกรวมกันว่า “ดวงจันทร์กาลิเลียน” ซึ่งหมายถึงดวงจันทร์บริวารของดาวพฤหัสบดีที่ค้นพบโดยคุณกาลิเลโอ กาลิเลอี ในปี พ.ศ. 2152 เราสังเกตเห็นดวงจันทร์เหล่านี้ได้ผ่านกล้องโทรทรรศน์

ภาพดวงจันทร์กาลิเลียนทั้ง 4 ดวง รอบดาวพฤหัสบดีที่ดูผ่านกล้องโทรทรรศน์
หรือหากไม่มีกล้องโทรทรรศน์ ก็สามารถสังเกตเห็นผ่านซอฟต์แวร์ Stellarium ได้เช่นเดียวกัน โดยดาวน์โหลดได้ฟรีที่ https://stellarium.org
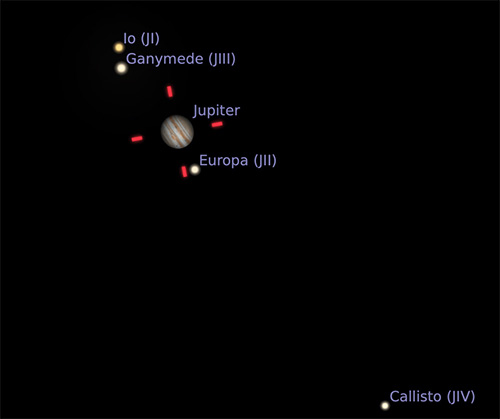
ภาพดวงจันทร์กาลิเลียนทั้ง 4 ดวงรอบดาวพฤหัสบดี ที่ดูผ่านซอฟต์แวร์ Stellarium
จากภาพด้านบนจะเห็นได้ว่าดวงจันทร์แต่ละดวงเรียงตัวกันตามระนาบการโคจรรอบดาวพฤหัสบดี ซึ่งทั้งสี่ดวงนี้จะโคจรในทิศเดียวกัน โดยหันเพียงหน้าเดียวเข้าหาดาวพฤหัสบดีตลอดเหมือนกันกับดวงจันทร์ของโลกเรา ปรากฏการณ์นี้เรียกว่า ความสัมพันธ์เชิงไทดัล (tidal locking) ที่รอบการโคจรของดวงจันทร์รอบดาวพฤหัสบดีนั้นใช้เวลาเท่ากับรอบการหมุนรอบตัวเองของดวงจันทร์
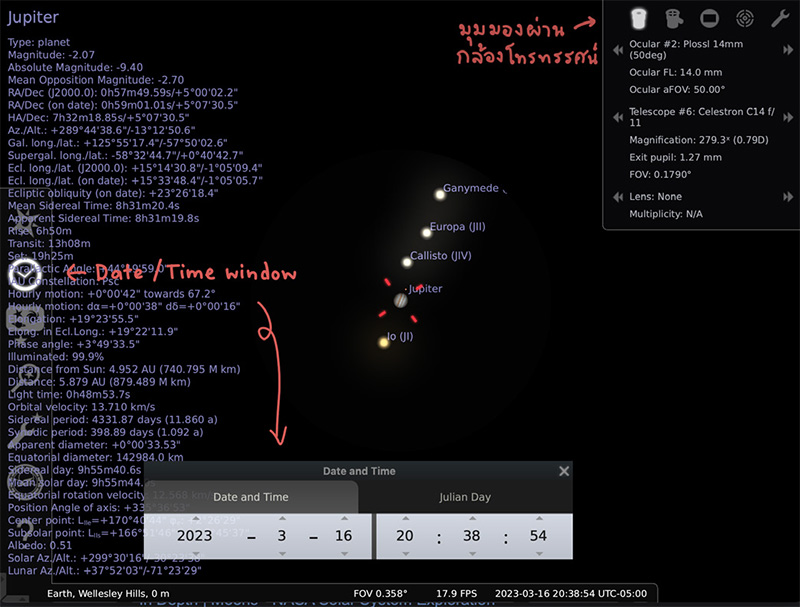
เมื่อเราลองปรับค่าในหน้าต่างวันและเวลาดังภาพด้านล่าง จะสังเกตได้ว่าดาวพฤหัสบดีและดวงจันทร์เปลี่ยนตำแหน่งไปเรื่อย ๆ เราสามารถกดปุ่มรูปกล้องโทรทรรศน์ที่มุมขวาบนเพื่อแสดงภาพที่เห็นได้ในกล้องโทรทรรศน์ตามรุ่นและกำลังขยายที่กำหนดได้สะดวกขึ้น ช่วยให้เราจับตามองดาวพฤหัสบดีขณะที่มันเคลื่อนที่ไปเรื่อย ๆ โดยไม่หลุดออกนอกกรอบการมองเห็น และยังคงเห็นการเคลื่อนที่ของดวงจันทร์กาลิเลียนทั้งสี่อีกด้วย
คราวนี้เราลองเปลี่ยนวันและเวลาดู จะพบว่ามีช่วงเวลาตอนพระอาทิตย์ขึ้นที่เราไม่สามารถสำรวจได้ หรือตอนที่ดาวพฤหัสบดีเคลื่อนที่ลงต่ำเกินไปจนถูกพื้นดินบดบัง ซึ่งในกรณีที่สังเกตผ่าน Stellarium เราสามารถตั้งค่าทำให้เสมือนว่าสังเกตดาวพฤหัสบดีในสภาพจำลองที่ไม่มีแสงอาทิตย์มารบกวนหรือมีพื้นดินมาบัง โดยตั้งค่าปิดการใช้งานพื้นดินและชั้นบรรยากาศออกเสียตามภาพ
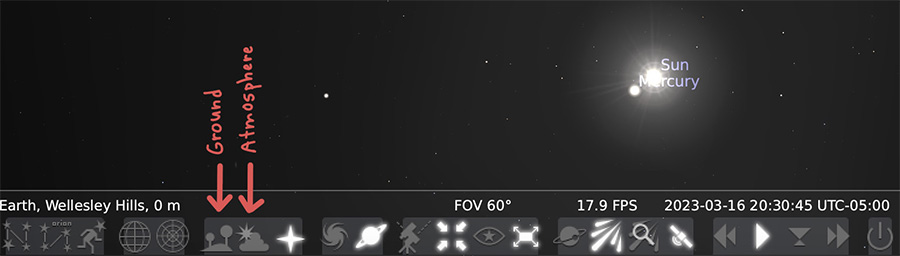
ภาพแสดงหน้าจอซอฟต์แวร์ Stellarium ที่ปิดการใช้งานพื้นดิน (Ground) และชั้นบรรยากาศ (Atmosphere)
เมื่อตั้งค่าการสำรวจเรียบร้อยแล้ว ก็มาเลือกกันก่อนว่าจะสังเกตวงโคจรของดวงจันทร์ดวงไหนดี สมมติว่าเราเลือกเป็น “ยูโรปา” คราวนี้กลับมาดูที่กฎข้อสามของเคปเลอร์กันอีกครั้ง มีใครจำกันได้บ้าง
แต่ในกรณีนี้ดวงจันทร์ของดาวพฤหัสบดีนั้นมีมวลต่ำมากเมื่อเทียบกับดาวพฤหัสบดี ในการคำนวณแบบคร่าวๆ เราจึงไม่จำเป็นต้องรวม m เข้าไปด้วยก็ได้)
จากสูตรคำนวณจะเห็นได้ว่ามี 2 ค่าที่เราต้องวัดผ่านการสำรวจ เพื่อหาคำตอบของค่า M หรือน้ำหนักของดาวพฤหัสบดี ได้แก่ 1) รัศมีวงโคจร ซึ่งคือค่าเฉลี่ยของระยะห่างระหว่างดาวพฤหัสบดีกับยูโรปา หรือความยาว semi-major axis ของวงโคจรของยูโรปานั่นเอง ในที่นี้เรากะได้เป็นระยะห่างระหว่างดาวพฤหัสบดีกับยูโรปา โดยวัดในขณะที่ยูโรปาอยู่ห่างจากดาวพฤหัสบดีมากที่สุด และ 2) คาบการโคจรของยูโรปา
1) รัศมีวงโคจร
การวัดระยะทางในเชิงดาราศาสตร์นั้นมีหลากหลายวิธีด้วยกัน ครั้งนี้ฉันขอลัดขั้นตอนด้วยการแอบกระซิบขนาดเส้นผ่านศูนย์กลางของดาวพฤหัสบดีให้ว่ามีค่าราว ๆ 0.001 เท่าของระยะห่างระหว่างโลกกับดวงอาทิตย์ (0.001 AU) แต่ระยะห่างที่เราต้องการคือระยะห่างระหว่างยูโรปากับดาวพฤหัสบดี วิธีที่ฉันแนะนำคือปรับเป็นค่าวันดูก่อน แล้วจึงค่อย ๆ ปรับในสเกลละเอียดลงมาเป็นค่าชั่วโมง และเมื่อถึงจุดที่ถ้าปรับไปมากกว่านี้ยูโรปาจะเริ่มวกโคจรกลับมาใกล้ดาวพฤหัสบดี นั่นแปลว่าเราได้มาถึง ณ จุดที่ไกลที่สุดแล้ว ฉันได้ทดลองเล่นปรับเวลาเพื่อศึกษาการโคจรของยูโรปาอยู่สักพัก จนประมาณตำแหน่งตอนที่ยูโรปาอยู่ไกลจากดาวพฤหัสบดีที่สุด
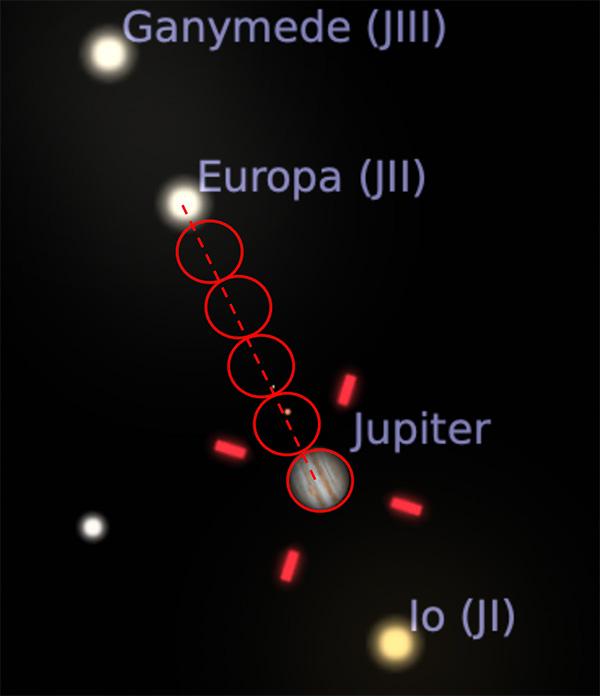
ตำแหน่งประมาณตอนที่ยูโรปาอยู่ไกลจากดาวพฤหัสบดีที่สุด
จากภาพ ฉันใช้ขนาดของดาวพฤหัสบดีมาเป็นสเกลวัดระยะห่างระหว่างดาวพฤหัสบดีถึงยูโรปา และพบว่าระยะนั้นคิดเป็นประมาณ 4.5 เท่าของเส้นผ่านศูนย์กลางดาวพฤหัสบดี ( 4.5×0.001 AU)
เมื่อแปลงหน่วยจากหน่วยดาราศาสตร์เป็นเมตรจะได้ดังนี้
2) คาบการโคจร
เพื่อวัดว่ายูโรปาใช้เวลานานแค่ไหนในการโคจรรอบดาวพฤหัสบดีครบหนึ่งรอบ เราสามารถเลือกจุดเริ่มต้นได้ตามใจชอบ ในที่นี้ฉันเลือกเป็นตำแหน่งที่ยูโรปาอยู่ไกลดาวพฤหัสบดีที่สุดตามที่ได้ใช้คำนวณระยะทางไปข้างต้น และคอยปรับวันเวลาไปทีละนิดเพื่อดูการเคลื่อนที่ของยูโรปารอบดาวพฤหัสบดี เวลาที่ผ่านไประหว่างจุดเริ่มต้นจนถึงจุดจบที่ยูโรปาโคจรกลับมาอยู่ ณ ตำแหน่งที่ระยะห่างจากดาวพฤหัสบดีเท่ากับตอนเริ่มต้นก็คือคาบการโคจรของยูโรปานั่นเอง
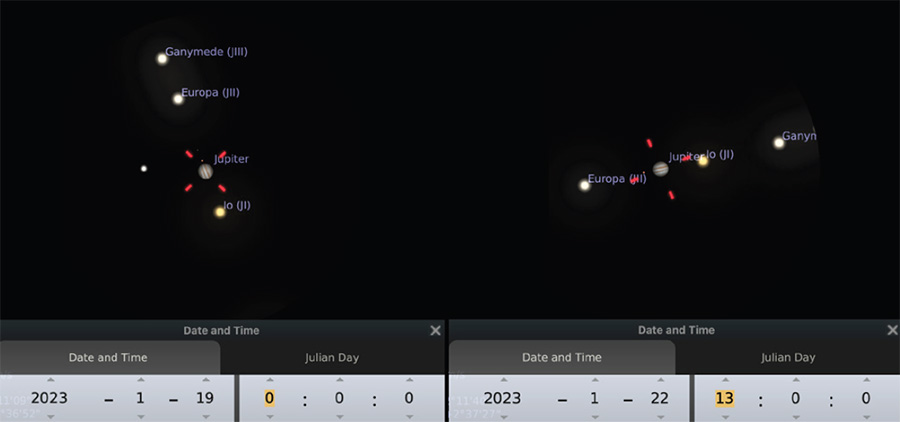
คาบการโคจรของยูโรปา ณ เวลาที่ผ่านไปจากจุดเริ่มต้นทางซ้ายถึงวันที่ครบรอบทางขวา ซึ่งวนกลับอยู่ตำแหน่งใกล้เดิม
จากภาพด้านบน ระยะเวลาที่ผ่านไประหว่างจุดเริ่มต้นกับจุดจบครบรอบวงโคจรมีค่าเท่ากับ 3 วัน กับอีก 13 ชั่วโมง หรือก็คือ 85 ชั่วโมง
เมื่อแปลงหน่วยจากชั่วโมงเป็นวินาที จะได้ดังนี้
ดาวพฤหัสบดีประกอบด้วยก๊าซไฮโดรเจนและฮีเลียมคล้ายดวงอาทิตย์ของเรา และหนาแน่นเพียง 1 ใน 4 ของความหนาแน่นของโลกเรา
ได้ผลสรุปว่า แม้ว่าดาวพฤหัสบดีจะมีความหนาแน่นน้อยแต่ก็ยังมากกว่าน้ำที่หนาแน่น 1 g/cm3 อยู่หน่อยหนึ่ง นั่นแปลว่าหากเราเอาดาวพฤหัสบดีมาลอยในอ่างน้ำยักษ์ ดาวพฤหัสบดีจะจมอย่างแน่นอน ! ซึ่งแตกต่างกับดาวเคราะห์ก๊าซเพื่อนบ้านอย่างดาวเสาร์ที่มีความหนาแน่นเพียง 0.687 g/cm3 จะลอยน้ำได้อย่างสบาย ๆ ฉันจึงใช้หลักจำง่าย ๆ ว่าดาวเสาร์มีห่วงยางวงแหวนรอบตัวเลยทำให้ลอยน้ำได้นั่นเอง
เทคโนโลยีจากซอฟต์แวร์ Stellarium ช่วยให้เราสามารถทำกิจกรรมสนุก ๆ เกี่ยวกับดาราศาสตร์ได้ในทุกที่ทุกเวลา ฝึกการใช้ข้อมูลที่มีอยู่เพื่อหาผลลัพธ์ที่ต้องการ และยังพิสูจน์กฎของเคปเลอร์ไปด้วยในตัว ซึ่งการพิสูจน์เป็นทักษะสำคัญยิ่งในการศึกษาวิทยาศาสตร์ไม่ว่าจะแขนงใด
เอาละ หากใครสนใจก็ลองไปเล่นกันดูนะ ลองเปลี่ยนดวงจันทร์ของดาวพฤหัสบดีเป็นดวงอื่นดูบ้าง อาจจะพบบางอย่างที่น่าสนใจ อย่างที่ฉันพบว่าคาบการโคจรของยูโรปาที่อยู่ใกล้ดาวพฤหัสบดีเป็นอันดับที่สองถัดจากไอโอ มีค่าเป็นสองเท่าของไอโอ และคาบการโคจรของแกนิมีดที่อยู่ใกล้ดาวพฤหัสบดีเป็นอันดับที่สาม มีค่าเป็นสี่เท่าของไอโออย่างเป๊ะ ๆ เลยด้วย หรือจะลองเปลี่ยนเป็นหามวลดาวเสาร์หรือดาวอื่น ๆ ที่มีบริวาร เพื่อเทียบผลคำนวณก็ได้เช่นกัน
หากสงสัยหรือสนใจอยากสอบถามข้อมูลเพิ่มเติมก็ทักทายกันมาได้นะ
ใครไปทดลองเล่นแล้วได้ผลออกมาเป็นอย่างไรก็มาแชร์กันได้ ฉันจะยินดีเป็นอย่างมาก แล้วพบกันใหม่ฉบับหน้า